Из страны пирамид

Весьма вероятно, что описанный способ дошел до нас из глубочайшей древности и из отдаленной страны - из Египта. Мы мало знаем, как производили арифметические действия обитатели древней Страны пирамид. Но сохранился любопытный документ - папирус, на котором записаны арифметические упражнения ученика одной из землемерных школ древнего Египта. - это так называемый "папирус Ринда", относящийся ко времени между 2000 и 1700 годом до нашей эры^* и представляющий собой копию еще более древней рукописи, переписанную неким Аамесом. Писец^** Аамес, найдя "ученическую тетрадку" этой отдаленнейшей эпохи, тщательно переписал все арифметические упражнения будущего землемера - вместе с их ошибками и исправлениями учителя - и дал своему списку торжественное заглавие, которое дошло до нас в следующем неполном виде:

„Наставление, как достигнуть 
знания всех темных вещей... 
всех тайн, сокрытых в вещах.
Составлено при царе Верхнего 
и Нижнего Египта Ра-а-усе, 
дающем жизнь, по образцу 
древних сочинений времен царя 
Ра-ен-мата писцом Аамесом".

^* (Папирус, заключенный в металлический футляр, был разыскан английским египтологом Генри Риндом. В развернутом виде имеет 20 м длины, при 30 см ширины. Хранится в Британском музее, в Лондоне.)

^** (Звание "писец" принадлежало третьему классу египетских жрецов; в заведывании их находилось "все относившееся к строительной части храма и к его земельной собственности". Математические, астрономические и географические знания составляли их главную специальность (В. Бобынин).)

Египетское изображение писца. Писцы в древнем Египте принадлежали к третьему классу жрецов; они заведовали землями и строительной частью храма. Обучение писца наукам, требующимся для этой должности, продолжалось 12 лет

В этом интересном документе, насчитывающем за собой около сорока веков и свидетельствующем о еще более глубокой древности, мы находим четыре примера умножения, выполненные по способу, живо напоминающему наш русский народный способ. Вот эти примеры (точки впереди чисел обозначают число единиц множителя; знаком + мы отметили числа, подлежащие сложению):

Вы видите из этих примеров, что еще за тысячелетия до нас египтяне пользовались приемом умножения, довольно сходным с нашим крестьянским, и что неведомыми путями он как бы перекочевал из древней Страны пирамид в современную эпоху. Если бы обитателю земли фараонов предложили перемножить, например, 19 X 17, он произвел бы это действие следующим образом: написал бы ряд последовательных удвоений числа 17

и затем сложил бы те числа, которые отмечены здесь знаком +, то-есть 17 + 34 + 272. Он получил бы, конечно, вполне правильный результат: 17 + (2 X 17) + (16 X 17) = 19 X 17. Легко видеть, что подобный прием по существу весьма близок к нашему крестьянскому (замена умножения рядом последовательных удвоений).

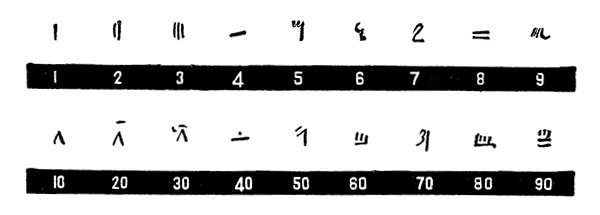
Египетские цифры иератического письма из папируса Ринда

Трудно сказать, у одних ли наших крестьян был в ходу такой древний способ умножения; английские авторы называют его именно "русским крестьянским способом"; в Германии крестьяне кое-где хотя и пользуются им, но также называют его "русским".

Чрезвычайно интересно было бы получить от читателей сведения о том, применяется ли сейчас где-нибудь этот древний способ умножения, имеющий за собой такое долгое и оригинальное прошлое. Следовало бы вообще с большим вниманием относиться к народной математике: вникать в употребляемые народом приемы счета и измерений, собирать и записывать эти памятники народного математического творчества, дошедшие до нашего времени из глубин седой старины.

На это давно указывал историк математики В. В. Бобынин^*, предложивший даже краткую программу собирания памятников народной математики. Не лишним будет, пожалуй, привести здесь составленный им перечень того, что именно следует собирать и записывать: 1) счисление и счет, 2) приемы меры и веса, 3) геометрические сведения и их выражение в постройках, нарядах и украшениях, 4) способы межевания, 5) народные задачи, 6) пословицы, загадки и вообще произведения народной словесности, имеющие отношение к математическим знаниям, 7) памятники древней народной математики, находящиеся в рукописях, музеях, коллекциях и т. д. или находимые при раскопках курганов, могил, городищ и проч.

^* (Бобынин В. В. (1849-1919) - первый историк математики в России.)