Пешки вместо цифр

После только что сказанного легко сообразить, что числа можно изображать не только с помощью цифр но и с помощью любых иных знаков или даже предметов: карандашей, перьев, линеек, резинок и т. п., надо только условиться приписывать каждому предмету значение какой-нибудь определенной цифры. Можно даже, ради курьеза, с помощью таких цифр-предметов изображать действия над числами: складывать, вычитать, умножать, делить.

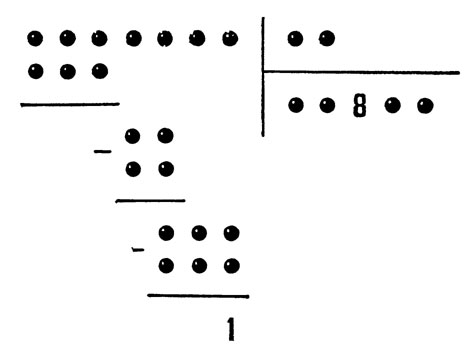
Попробуйте доискаться значения всех цифр этого деления!

В одном зарубежном шахматном журнале была предложена задача: раскрыть истинный смысл следующего примера деления чисел, в котором почти все цифры заменены пешками (на нашем рисунке - черными кружками). Из 28 цифр известны только две: одна (8) в частном и другая (1) в остатке. Казалось бы, доискаться значения прочих 26 цифр, обозначенных кружками, немыслимо. Между тем это сравнительно несложная задача для каждого, кто отчетливо представляет себе смысл отдельных операций, входящих в состав действия деления.

Вот какой ход рассуждений приводит нас к цели.

Вторая цифра частного есть, конечно, 0. Это следует из того, что к остатку от первого вычитания снесена не одна цифра, а две: ясно, что после снесения первой цифры составилось число, меньшее делителя; а в таких случаях очередная цифра частного 0.

По сходным основаниям заключаем, что четвертая цифра частного также 0.

Всматриваясь в расположение кружочков, замечаем, что двузначный делитель, будучи умножен на 8, дает число двузначное; когда же его умножают на первую (пока неизвестную) цифру частного, получается число из трех цифр. Значит, эта первая цифра частного больше 8; такой цифрой может быть только 9.

Сходным образом устанавливаем, что и последняя цифра частного - 9.

Теперь частное определилось: 90809. Остается раскрыть смысл делителя. Делитель состоит, мы знаем, из двух цифр; кроме того, расположение кружков говорит о том, что это двузначное число при умножении на 8 дает также двузначное число; при умножении же на 9 оно дает произведение, состоящее уже из трех цифр. Что же это за число? Производим испытания, начиная с наименьшего двузначного числа - 10:

 10 X 8 = 80, 
 10 X 9 = 90.

Число 10, как видим, не удовлетворяет требуемым условиям: оба произведения двузначные. Испытываем следующее двузначное число - 11:

 11 X 8 = 88, 
 11 X 9 = 99.

Число 11 также, очевидно, не годится: оба произведения снова двузначные. Испытываем 12:

 12 X 8 = 96, 
 12 X 9 = 108.

Число 12 удовлетворяет всем требованиям. Нет ли еще таких чисел? Испытаем 13:

 13 X 8 = 104, 
 13 X 9 = 117. 

Оба произведения трехзначные; следовательно, 13 не годится. Ясно, что неподходящими являются и все числа, большие чем 13.

Итак, единственный возможный делитель - 12. Зная делитель, частное и остаток, легко находим делимое и восстанавливаем весь случай деления.

Итак,

делимое = 90 809 X 12 + 1 = 1089709.

Случай деления:

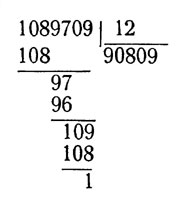
Как видим, по двум известным цифрам нам удалось установить смысл 26 неизвестных цифр.