
Арифметика за завтраком
Перед нами ряд действий над числами, обозначенными предметами сервировки стола (см. рисунок). Вилка, ложка, нож, кувшинчик, тарелка - все это знаки, каждый из которых заменяет определенную цифру.
Глядя на эту группу ножей, вилок, посуды и т. п., попробуйте угадать: какие именно числа здесь обозначены?
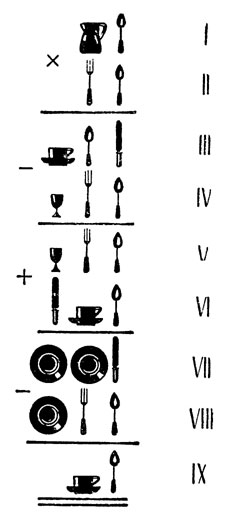
Разгадайте, над какими числами производятся обозначенные здесь арифметические действия!
С первого взгляда задача кажется очень трудной: приходится разгадывать настоящие иероглифы*, как сделал некогда француз Шампольон**. Но ваша задача гораздо легче. Вы ведь знаете, что числа здесь, хотя обозначены вилками, ножами, ложками и т. п., написаны по десятичной системе счисления, то-есть вам известно, что тарелка, стоящая на втором месте (считая справа), есть цифра десятков, что предмет направо от нее - цифра единиц, а по левую сторону - цифра сотен. Кроме того, вы знаете, что расположение всех этих предметов имеет определенный смысл, который вытекает из сущности арифметических действий, производимых над обозначенными ими числами. Все это может значительно облегчить вам решение предложенной задачи.
* (Иероглиф - фигурный знак, обозначающий или целые понятия, или отдельные слоги и звуки речи.)
** (Шампольон (1790-1832) - знаменитый французский филолог, основатель египтологии - науки, изучающей язык, историю и культуру древнего Египта и прилегающих к нему стран.)
Вот как можно доискаться значения расставленных здесь предметов. Рассматривая первые три ряда на нашем рисунке, вы видите, что "ложка", умноженная на "ложку", дает "нож". А из следующих рядов видно, что "нож" без "ложки" дает "ложку" или что "ложка", прибавленная к "ложке", дает "нож". Какая же цифра дает одно и то же и при удвоений и при умножении сама на себя? Это может быть только 2, потому что 2 X 2 = 2 + 2. Таким образом узнаём, что "ложка" обозначает 2 и, следовательно, "нож" - 4.
Теперь идем дальше. Какая цифра обозначена "вилкой"? Попробуем разгадать это, присмотревшись к первым трем рядам, где "вилка" участвует в умножении, и к рядам III, IV и V, где та же "вилка" фигурирует в действии вычитания. Из группы вычитания вы видите, что, отнимая в разряде десятков "вилку" от "ложки", получаем в результате "вилку", то-есть при вычитании "вилки" из двойки получается "вилка". Это может быть в двух случаях: либо "вилка" обозначает 1, и тогда 2-1 = 1; либо же "вилка" обозначает 6, и тогда, вычитая 6 из 12 (единица высшего разряда занимается у "чашки"), получаем 6.
Что же выбрать: 1 или 6? Испытаем, годится ли 6 для "вилки" в других действиях. Обратите внимание на сложение V и VI рядов: "вилка" (то-есть 6), прибавленная к "чашке", дает "тарелку"; значит, "чашка" должна быть меньше 4 (потому что в рядах VII и VIII при вычитании "вилки" из "тарелки" получается "чашка"). Но "чашка" не может обозначаться двойкой, так как двойка обозначена уже "ложкой"; не может "чашка" быть и единицей - иначе вычитание IV ряда из III не могло бы дать трехзначного числа в V ряду. Не может, наконец, "чашка" обозначать и 3 - вот почему: если "чашку" принять за 3, то "бокальчик" (ряды IV и V) должен быть принят за единицу, потому что 1 + 1 = 2, то-есть "бокальчик", прибавленный к "бокальчику", дает "чашку", убавленную на единицу, которая была занята у него при вычитании в разряде десятков; "бокальчик" же не может быть принят за единицу, потому что тогда "тарелка" в VII ряду будет обозначать в одном случае цифру 5 ("бокальчик", сложенный с "ножом"), а в другом - цифру 9 ("вилка", прибавленная к "чашке"), чего быть не может. Значит, нельзя было "вилку" принимать за 6, а надо было принять ее за единицу.
Узнав путем таких - довольно, правда, долгих - поисков, что "вилка" обозначает цифру 1, мы дальше идем более уверенно и быстро. Из действия вычитания в III и IV рядах видим, что "чашка" обозначает либо 6, либо 8. Но 8 приходится отвергнуть, потому что тогда вышло бы, что "бокальчик" должен обозначать 4, а мы знаем, что цифра 4 обозначена "ножом". Итак, "чашка" обозначает цифру 6, а следовательно, "бокальчик" - цифру 3.
Какая же цифра обозначена "кувшинчиком" в I ряду? Это легко узнать, раз нам известно произведение (III ряд, 624) и один из множителей (ТУ ряд, 12). Разделив 624 на 12, получаем 52. Следовательно, "кувшинчик" обозначает 5.
Значение "тарелки" определяется просто: в VII ряду "вилка", прибавленная к "чашке", и "бокальчик", прибавленный к "ножу", дают порознь "тарелку", то-есть "тарелка" обозначает число, равное 1 + 6 = 3 + 4 = 7.
Итак, мы путем нехитрых арифметических вычислений разгадали иероглифическую надпись из предметов столовой сервировки:
"кувшин" обозначает 5, "ложка" обозначает 2, "вилка" обозначает 1, "нож" обозначает 4, "чашка" обозначает 6, "бокальчик" обозначает 3, "тарелка" обозначает 7.
А весь ряд арифметических действий, изображенный этой оригинальной сервировкой, приобретает такой смысл:
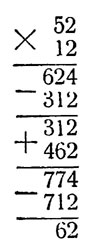
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'