Глава II. Основные положения преподавания математики

1. О содержании математических курсов

Как это ни странно, уже само понимание предмета математики, а значит, его содержание и расстановка в нем акцентов, вызывает разногласие. Мы будем исходить из следующего основного положения.

Положение первое. В курсе математики изучаются математические модели.

Как уже говорилось, объектами изучения в математике являются не реальные явления, а абстрактные логические объекты и структуры, у которых описан ряд отношений между их элементами (будем их коротко, как и прежде, называть математическими моделями), не размерные величины, а безразмерные. Математика изучает соотношения между элементами математических моделей, количественные и качественные связи между ними. Для математики важна не природа рассматриваемых объектов, а лишь имеющиеся между ними соотношения. Одна и та же математическая модель может описывать (с определенным приближением) свойства очень далеких друг от друга по своему конкретному содержанию реальных явлений. Так, например, формула

может описывать и закон Ньютона притяжения масс и закон Кулона притяжения электрических зарядов. Величины масс и зарядов, фигурирующие в этих законах, измеряются в разных единицах, имеют разную размерность. В математической же формуле соответствующие этим законам математические операции (в данном случае умножение и деление) производятся по правилам действия над числами, независимо от того, значениями каких физических величин они являются.

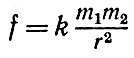
Из сформулированного положения следует, что смысл математического понятия не зависит от области его дальнейшего применения, в частности, не зависит от специализации студента, которому разъясняется это понятие.

При этом следует подчеркнуть различие смысла и содержания математического понятия как такового и конкретного явления, для описания которого оно используется, например, понятия производной векторной функции и понятия скорости механического движения, понятия интеграла и понятия работы и т. п.

Сущность математики должна находить свое отражение при обучении математике прежде всего в разъяснении истинного смысла изучаемых математических понятий.

Это утверждение, кажущееся многим бесспорным, тем не менее часто оспаривается. Некоторые считают, что те, кто интересуется математикой не самой по себе, а лишь математическими методами исследования конкретных задач, т. е. приложениями математики, должны обучаться специальной математике, а не той, которой занимаются сами математики. На самом деле такой специальной математики не существует. Смысл теоремы Пифагора или формулы конечных приращений Лагранжа не зависит от того, кто их использует: инженер или научный работник, прикладник или чистый математик. От будущей специальности студента зависну лишь содержание и объем курса математики, отбор математических понятий и фактов, отбор методов, общность и детализация изложения, подбор примеров, иллюстрирующих применение изучаемых математических понятий и методов к решению прикладных задач.

Можно в принципе учить приложениям математики вместо самой математики, исходя из будущей специализации. Говорить, например, будущим механикам, что производная есть механическая скорость, что интеграл - работа силы, и рассматривать только размерные величины. Конечно, это будет уже не математика. Возможно, в отдельных случаях (крайне редких, которые даже трудно себе представить) это может оказаться целесообразным. В основном же такой метод обучения плох тем, что человек, изучавший такой специализированный курс, окажется беспомощным, когда он встретится с неизучавшейся им конкретной ситуацией, несмотря на то, что она будет требовать для ее описания или изучения, по существу, того же самого математического аппарат та, которому его обучали на конкретных примерах. Он будет беспомощен, поскольку он не был обучен общему подходу, не был приучен к рассмотрению абстрактных математических моделей.

Не случайно в настоящее время наблюдается ярко выраженная упоминавшаяся выше тенденция сближения университетского и высшего технического образования на основе более общего подхода к изучаемым предметам. Современные темпы развития науки и техники таковы, что в силу быстрого изменения конкретных условий работы делается не выгодным готовить узких специалистов. Сейчас все больше потребность в специалистах, которые могут быстро ориентироваться при изменении ситуации, способны правильно оценивать происходящие изменения, приводящие иной раз к качественно совершенно новым явлениям. Эти качества прививаются не узко специальным образованием, а широким общим образованием университетского типа. Уже сейчас во многих передовых высших учебных заведениях, готовящих специалистов по современной науке и технике, математические (а также физические, химические и др.) курсы изучаются по одинаковой программе, не зависящей от будущей специальности студента (например, физической, химической, аэродинамической и т п.).

Много говорится и о том, что учить математике инженеров надо своими особыми методами, не так, как это делают математики. Этот вопрос мы рассмотрим позже, когда будем обсуждать вопросы методики преподавания.

Все сказанное здесь предполагает, безусловно, что рассматриваемые математические понятия изучаются для их дальнейшего использования при математических методах исследования тех или иных вопросов. В случае же, когда знакомятся с математическими понятиями лишь с целью использования их для описания конкретного явления, часто нет нужды разбираться в смысле используемого математического понятия, и можно ограничиться знакомством с ним на интуитивном уровне. На этом вопросе мы также остановимся подробнее ниже, когда будем обсуждать пятое положение.