Алгебра на клетчатой бумаге

Несмотря на пятидесятивековую древность этой задачи на прогрессии, в нашем школьном обиходе прогрессии появились сравнительно недавно. В учебнике Магницкого, изданном двести лет назад и служившем целых полвека основным руководством для школьного обучения, прогрессии хотя и имеются, но общих формул, связывающих входящие в них величины между собой, в нем не дано. Сам составитель учебника не без затруднений справлялся поэтому с такими задачами. Между тем формулу суммы членов арифметической прогрессии легко вывести простым и наглядным приемом с помощью клетчатой бумаги. На такой бумаге любая арифметическая прогрессия изображается ступенчатой фигурой. Например, фигура ABDC на рис. 33 изображает прогрессию:

2; 5; 8; 11; 14.

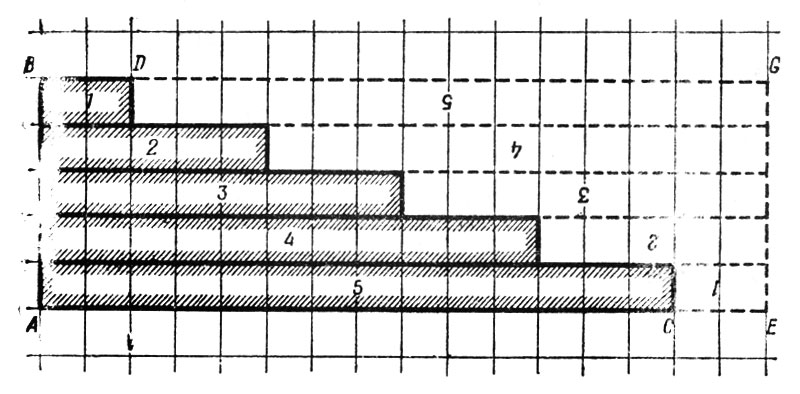
Рис. 33. Фигура ABDC

Чтобы определить сумму ее членов, дополним чертеж до прямоугольника ABGE. Получим две равные фигуры ABDC и DGEC. Площадь каждой из них изображает сумму членов нашей прогрессии. Значит, двойная сумма прогрессии равна площади прямоугольника ABGE, т. е.

(АС + СЕ) × АВ.

Но АС + СЕ изображает сумму 1-го и 5-го членов прогрессии; АВ - число членов прогрессии. Поэтому двойная сумма

2S = (сумма крайних членов) × (число членов)

или

S =  ((первый + последний член) × (число членов))/2.