Глава VIII. Прогрессии

Древнейшая прогрессия

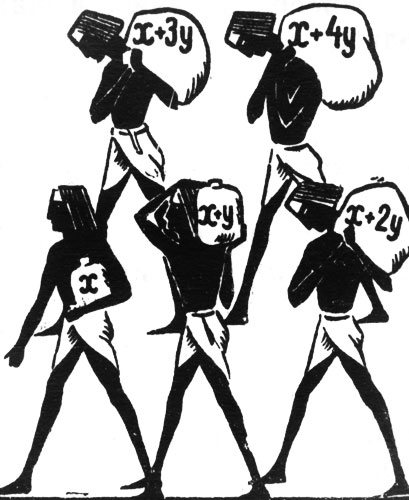
Прогрессии

Задача

Древнейшая задача на прогрессии - не вопрос о вознаграждении изобретателя шахмат, насчитывающий за собой двухтысячелетнюю давность, а гораздо более старая задача о делении хлеба, которая записана в знаменитом египетском папирусе Ринда. Папирус этот, разысканный Риндом в конце прошлого столетия, составлен около 2000 лет до нашей эры и является списком с другого, еще более древнего математического сочинения, относящегося, быть может, к третьему тысячелетию до нашей эры. В числе арифметических, алгебраических и геометрических задач этого документа имеется такая (приводим ее в вольной передаче):

Сто мер хлеба разделить между пятью людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго, четвертый больше третьего и пятый больше четвертого. Кроме того, двое первых должны получить в 7 раз меньше трех остальных. Сколько нужно дать каждому?

Решение

Очевидно, количества хлеба, полученные участниками раздела, составляют возрастающую арифметическую прогрессию. Пусть первый ее член х, разность y. Тогда

 доля первого     х 
 доля второго     х + у 
 доля третьего    х + 2y 
 доля четвертого  х + 3y 
 доля пятого      х + 4y.

На основании условий задачи составляем следующие два уравнения:

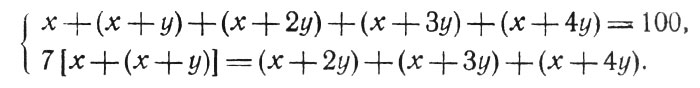
После упрощений первое уравнение получает вид

x + 2y = 20,

а второе:

11х = 2y.

Решив эту систему, получаем:

x = 1 2/3, y = 9 1/6.

Значит, хлеб должен быть разделен на следующие части

1 2/3, 10 5/6, 20, 29 1/6, 38 1/3.