Самое яркое освещение

Задача

На какой высоте над столом должно находиться пламя свечи, чтобы всего ярче освещать лежащую на столе монету?

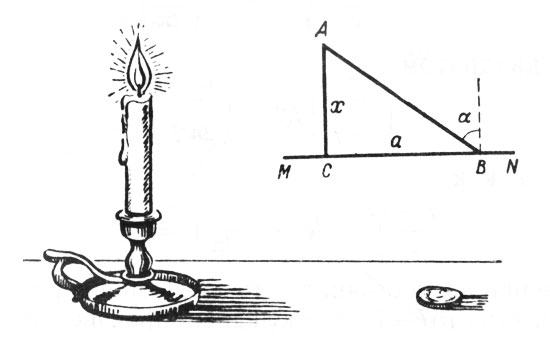
Рис. 32. На какой высоте над столом должно находиться пламя свечи, чтобы всего ярче освещать лежащую на столе монету?

Решение

Может показаться, что для достижения наилучшего освещения надо поместить пламя возможно ниже. Это неверно: при низком положении пламени лучи падают очень отлого. Поднять свечу так, чтобы лучи падали круто, - значит удалить источник света. Наиболее выгодна в смысле освещения, очевидно, некоторая средняя высота пламени над столом. Обозначим ее через х (рис. 32). Расстояние ВС монеты В от основания С перпендикуляра, проходящего через пламя А, обозначим через а. Если яркость пламени i, то освещенность монеты согласно законам оптики выразится так:

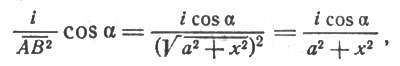
где α - угол падения пучка лучей АВ. Так как

                           ________
cos α =  cos A = x/AB = x/√(a2 + x2),

то освещенность равна

                 ________
i/(а2 + х2) × x/	√(a2 + x2) = ix/(a2 + x2)3/2.

Это выражение достигает максимума при том же значении х, что и его квадрат, т. е.

i2x2/(a2 + x2)3.

Множитель i² как величину постоянную опускаем, а остальную часть исследуемого выражения преобразуем так:

x2/(a2 + x2)3 = 1/(x2 + a2)2 × (1 - a2/(x2 + a2)) = (1/(x2 + a2))2 × (1 - a2/(x2 + a2)). 

Преобразованное выражение достигает максимума одновременно с выражением

(a2/(x2 + a2))2 × (1 - a2/(x2 + a2)).

так как введенный постоянный множитель а4 не влияет на то значение х, при котором произведение достигает максимума. Замечая, что сумма первых степеней этих множителей

a2/(x2 + a2) + (1 - a2/(x2 + a2)) = 1

есть величина постоянная, заключаем, что рассматриваемое произведение становится наибольшим, когда

a2/(x2 + a2) : (1 - a2/(x2 + a2)) = 2 : 1

Имеем уравнение

а2 = 2x2 + 2а2 - 2а2. 

Решив это уравнение, находим:

       _
x = a/√2 ≈ 0,71a.

Монета освещается всего ярче, когда источник света находится на высоте 0,71 расстояния от проекции источника до монеты. Знание этого соотношения помогает при устройстве наилучшего освещения рабочего места.