Воронка наибольшей вместимости

Задача

Из жестяного круга нужно изготовить коническую часть воронки. Для этого в круге вырезают сектор и остальную часть круга свертывают конусом (рис. 31).

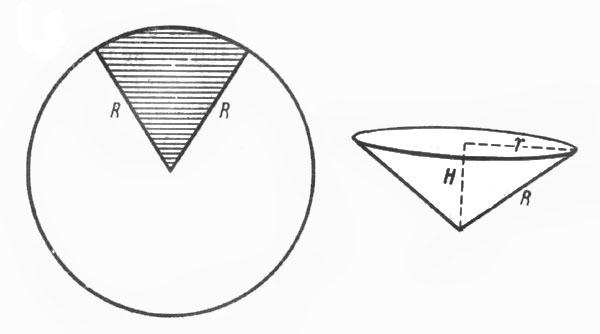
Рис. 31. Из жестяного круга нужно изготовить коническую часть воронки. Для этого в круге вырезают сектор и остальную часть круга свертывают конусом

Сколько градусов должно быть в дуге вырезаемого сектора, чтобы конус получился наибольшей вместимости?

Решение

Длину дуги той части круга, которая свертывается в конус, обозначим через х (в линейных мерах). Следовательно, образующей конуса будет радиус R жестяного круга, а окружность основания будет равна х. Радиус r основания конуса определяем из равенства

2πr = х, откуда r = x/2π.

Высота конуса (по теореме Пифагора)

     ________     _____________
H = √(R2 - r2) = √(R2 - x2/(4π2))

(рис. 31). Объем этого конуса имеет значение

                           _____________
V = π/3 r2H = π/3 (x/2π)2 √(R2 - x2/(4π2)).

Это выражение достигает наибольшей величины одновременно с выражением

         _______________
(x/2π)2 √(R2 - (x/(2π))2)

и его квадратом

(x/2π)4 [R2 - (x/2π)]

Так как

(x/2π)2 + R2 - (x/2π)2 = R2

есть величина постоянная, то последнее произведение имеет максимум при том значении х, когда

(x/2π)2 : [R2 - (x/2π)2] = 2 : 1,

откуда

(x/2π)2 = 2R2 - 2(x/2π)2,
                             _
3(x/2π)2 = 2R2 и  x = 2π/3 R√6 ≈ 5,15R.

В градусах дуга x ≈ 295° и, значит, дуга вырезаемого сектора должна содержать ≈ 65°.