Желоб наибольшего сечения

Задача

Рис. 27. Прямоугольный металлический лист

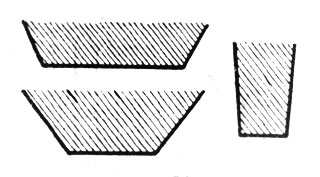
Рис. 28. Прямоугольный металлический лист надо согнуть желобом с сечением в форме равнобокой трапеции

Прямоугольный металлический лист (рис. 27) надо согнуть желобом с сечением в форме равнобокой трапеции. Это можно сделать различными способами, как видно из рис. 28. Какой ширины должны быть боковые полосы и под каким углом они должны быть отогнуты, чтобы сечение желоба имело наибольшую площадь (рис. 29)?

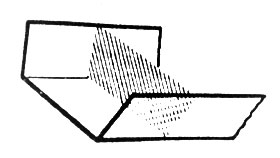
Рис. 29. Какой ширины должны быть боковые полосы и под каким углом они должны быть отогнуты, чтобы сечение желоба имело наибольшую площадь

Решение

Пусть ширина листа l. Ширину отгибаемых боковых полос обозначим через х, а ширину дна желоба - через y. Введем еще одно неизвестное z, значение которого ясно из рис. 30.

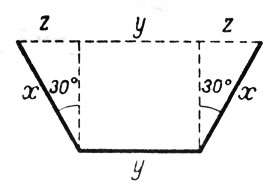
Рис. 30. Пусть ширина листа l. Ширину отгибаемых боковых полос обозначим через х, а ширину дна желоба - через y. Введем еще одно неизвестное z

Площадь трапеции, представляющей сечение желоба,

                           ________     ________________
S = ((z + у + z) + у)/2 × √(x2 - z2) = √(y + z)2(x2 - z2).

Задача свелась к определению тех значений х, y, z, при которых S достигает наибольшей величины; при этом сумма 2х + y (т. е. ширина листа) сохраняет постоянную величину l. Делаем преобразования:

S2 =(y + z)2(x + z)(x - z).

Величина S² становится наибольшей при тех же значениях х, y, z, что и 3S², последнюю же можно представить в виде произведения

(y + z)(y + z)(x + z)(3x - 3z).

Сумма этих четырех множителей

y + z + y + z + x + z + 3x - 3z = 2y + 4x = 2l,

т. е. неизменна. Поэтому произведение наших четырех множителей максимально, когда они равны между собой, т. е.

y + z = x + z и x + z = 3x - 3z

Из первого уравнения имеем:

y = х,

а так как y + 2х = l, то х = у = l/3.

Из второго уравнения находим:

z = x/2 = l/6.

Далее, так как катет z равен половине гипотенузы х (рис. 30), то противолежащий этому катету угол равен 30°, а угол наклона боков желоба ко дну равен 90° + 30° = 120°.

Итак, желоб будет иметь наибольшее сечение, когда грани его согнуты в форме трех смежных сторон правильного шестиугольника.