Дачный участок

Задача

При постройке дачи нужно было отгородить дачный участок. Материала имелось на l погонных метров изгороди. Кроме того, можно было воспользоваться ранее построенным забором (в качестве одной из сторон участка). Как при этих условиях отгородить прямоугольный участок наибольшей площади?

Решение

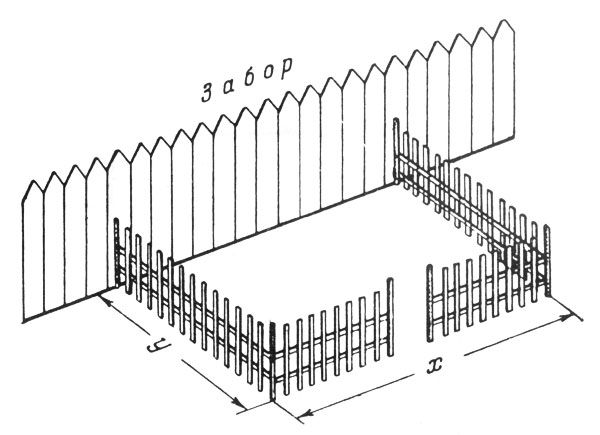
Рис. 26. Пусть длина участка (по забору) равна х, а ширина (т. е. размер участка в направлении, перпендикулярном к забору) равна y

Пусть длина участка (по забору) равна х, а ширина (т. е. размер участка в направлении, перпендикулярном к забору) равна y (рис. 26). Тогда для огораживания этого участка нужно х + 2y метров изгороди, так что

х + 2y = l.

Площадь участка равна

S = xy = y(l - 2y).

Она принимает наибольшее значение одновременно с величиной

2y(l - 2y)

(удвоенной площадью), которая представляет собой произведение двух множителей с постоянной суммой/. Поэтому для достижения наибольшей площади должно быть

2y = l - 2у,

откуда

y = l/4, x = l - 2y = l/2.

Иначе говоря, х = 2y, т. е. длина участка должна быть вдвое больше его ширины.