Постройка дома

Задача

На месте разрушенного дома, от которого уцелела одна стена, желают построить новый. Длина уцелевшей стены - 12 м. Площадь нового дома должна равняться 112 кв. м. Хозяйственные условия работы таковы:

1. ремонт погонного метра стены обходится в 25% стоимости кладки новой;
2. разбор погонного метра старой стены и кладка из полученного материала новой стены стоит 50% того, во что обходится постройка погонного метра стены из нового материала.

Как при таких условиях наивыгоднейшим образом использовать уцелевшую стену?

Решение

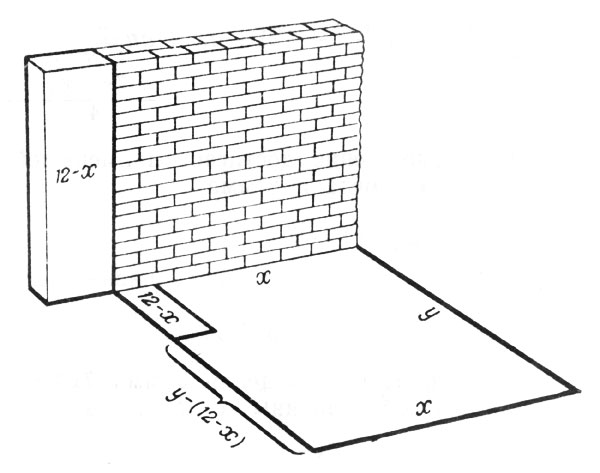
Рис. 25. Пусть от прежней стены сохраняется х метров, а остальные 12 - х метров разбираются, чтобы из полученного материала возвести заново часть стены нового дома

Пусть от прежней стены сохраняется х метров, а остальные 12 - х метров разбираются, чтобы из полученного материала возвести заново часть стены нового дома (рис. 25). Если стоимость кладки погонного метра стены из нового материала равна а, то ремонт х метров старой стены будет стоить ax/4; возведение участка длиной 12 - х будет стоить a(12 - x)/2; прочей части этой стены а[y -(12-х)], т. е. а(y + х - 12); третьей стены ах, четвертой аy. Вся работа обойдется в

ax/4 + (a(12 - x))/2 + a(y + x -12) + ax + ay = (a(7x + 8y)/4 - 6a.

Последнее выражение достигает наименьшей величины тогда же, когда и сумма

7х + 8y.

Мы знаем, что площадь дома хy равна 112; следовательно,

7х × 8y = 56 × 112.

При постоянном произведении сумма 7х + 8y достигает наименьшей величины тогда, когда

7х = 8y,

откуда

y = 7/8x.

Подставив это выражение для y в уравнение

xy = 112,

имеем:

                  ___
7/8x2 = 112, x = √128 ≈ 11,3.

А так как длина старой стены 12 м, то подлежит разборке только 0,7 м этой стены.