Бумажный змей

Задача

Змею, имеющему вид кругового сектора, желают придать такую форму, чтобы он вмещал в данном периметре наибольшую площадь. Какова должна быть форма сектора?

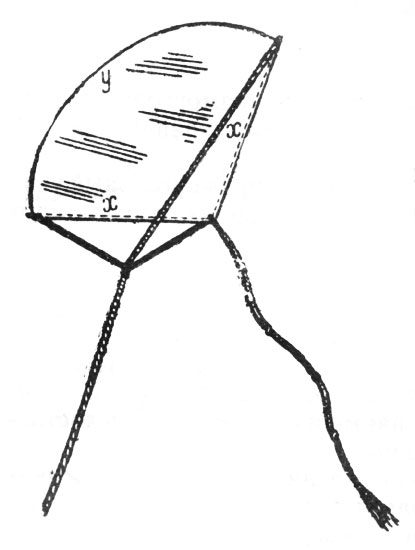
Рис. 24. Змею, имеющему вид кругового сектора, желают придать такую форму, чтобы он вмещал в данном периметре наибольшую площадь

Решение

Уточняя требование задачи, мы должны разыскать, при каком соотношении длины дуги сектора и его радиуса площадь его достигает наибольшей величины при данном периметре.

Если радиус сектора х, а дуга y, то его периметр l и площадь S выразятся так (рис. 24):

      l = 2х + y, 

 S = xy/2 = х(l - 2х)/2.

Величина S достигает максимума при том же значении х, что и произведение 2х (l - 2х), т. е. учетверенная площадь. Так как сумма множителей 2х+(l - 2х) = l есть величина постоянная, то произведение их наибольшее, когда 2х = l - 2х, откуда

        x = l/4, 

 y = l - 2 × l/4 = l/2.

Итак, сектор при данном периметре замыкает наибольшую площадь в том случае, когда его радиус составляет половину дуги (т. е. длина его дуги равна сумме радиусов или длина кривой части его периметра равна длине ломаной). Угол сектора равен ≈ 115° - двум радианам. Каковы летные качества такого широкого змея, - вопрос другой, рассмотрение которого в нашу задачу не входит.