Как провести шоссе?

Задача

Из приречного города А надо направлять грузы в пункт В, расположенный на а киломертов ниже по реке и в d километрах от берега (рис. 22). Как провести шоссе от В к реке, чтобы провоз грузов из А в В обходился возможно дешевле, если провозная плата с тонно-километра по реке вдвое меньше, чем по шоссе?

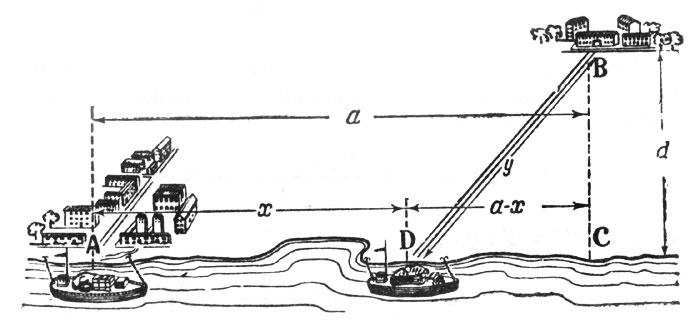
Рис. 22. Из приречного города А надо направлять грузы в пункт В, расположенный на а киломертов ниже по реке и в d километрах от берега

Решение

Обозначим расстояние AD через х и длину DB шоссе - через у: по предположению, длина АС равна а и длина ВС равна d.

Так как провоз по шоссе вдвое дороже, чем по реке, то сумма

х + 2у

должна быть согласно требованию задачи наименьшая. Обозначим это наименьшее значение через m. Имеем уравнение

х + 2у = m.

Но x = a - DC, a

      ________
DC = √(y2 - d2); наше уравнение получает вид 

     ________
а - √(у2 - d2) + 2у = m,

или по освобождении от радикала:

3у2 - 4(m - а)у + (m - a)2 + d2 = 0.

Решаем его:

                  _______________
y = 2/3(m - a) ± √((m - a)2 - 3d2)/3.

Чтобы y было действительным, (m - а)² должно быть не меньше 3d². Наименьшее значение (m - a)² равно 3d², и тогда

          _                            _
m - a = d√3, y = (2(m - a) + 0)/3 = 2d√3/3;

sin ∠ BDC = d : y, т. е.

                          _      _
sin ∠ BDC = d/y = d : 2d√3/3 = √3/2.

                                _
 Но угол, синус которого равен √3/2, равен 60°. 

Значит, шоссе надо провести под углом в 60° к реке, каково бы ни было расстояние АС.

Здесь наталкиваемся снова на ту же особенность, с которой мы встретились в предыдущей задаче. Решение имеет смысл только при определенном условии. Если пункт расположен так, что шоссе, проведенное под углом в 60° к реке, пройдет по ту сторону города А, то решение неприложимо; в таком случае надо непосредственно связать пункт В с городом А шоссе, вовсе не пользуясь рекой для перевозки.