Где устроить полустанок?

Задача

В стороне от прямолинейного участка железнодорожного пути, в 20 км от него, лежит селение В (рис. 21). Где надо устроить полустанок С, чтобы проезд от A до B по железной дороге АС и по шоссе СВ отнимал возможно меньше времени? Скорость движения по железной дороге 0,8, а по шоссе 0,2 километра в минуту.

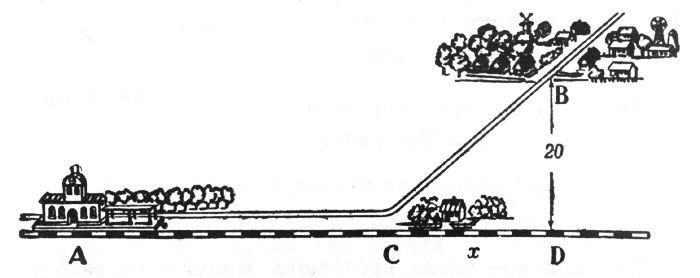
Рис. 21. В стороне от прямолинейного участка железнодорожного пути, в 20 км от него, лежит селение В

Решение

Обозначим расстояние AD (от A до основания перпендикуляра BD к AD) через a, CD через х. Тогда

                              __________     _________
AC = AD - CD = a - x, а CB = √(CD2 + BD2) = √(x2 + 202).

Время, в течение которого поезд проходит путь AC, равно

АС/0,8 = (a - x)/0,8.

Время прохождения пути СВ по шоссе равно

          _________
СВ/0,2 = √(x2 + 202)/0,2.

Общая продолжительность переезда из A в B равна

               _________
(a - x)/0,8 + √(x2 + 202)/0,2.

Эта сумма, которую обозначим через m, должна быть наименьшей.

Уравнение

               _________
(a - x)/0,8 + √(x2 + 202)/0,2 = m

представляем в виде

          _________
-x/0,8 + √(x2 + 202)/0,2 = m - a/0,8.

Умножив на 0,8, имеем:

       _________
-x + 4√(x2 + 202) = 0,8m - a.

Обозначив 0,8m - а через k и освободив уравнение от радикала, получаем квадратное уравнение

15х2 - 2kx + 6400 - k2 = 0,

откуда

          _____________
x = (k ± √(16k2 - 96000))/15. 

Так как k = 0,8m - а, то при наименьшем значении m достигает наименьшей величины и k, и обратно*. Но чтобы х было действительным, 16k² должно быть не меньше 96000. Значит, наименьшая величина для 16k² есть 96000. Поэтому m становится наименьшим, когда

16k2 = 96000,

откуда

     ____
k = √6000,

и следовательно,

                  ____
x = (k ± 0)/15 = √6000/15 ≈ 5,16.

^* (Следует иметь в виду, что k > 0, так как

                 _________
0,8m = а - х + 4√(x2 + 202) > a - х + х = а.

)

Полустанок должен быть устроен приблизительно в 5 км от точки D, какова бы ни была длина a = AD.

Но, разумеется, наше решение имеет смысл только для случаев, когда х < а, так как, составляя уравнение, мы считали выражение а - х числом положительным.

Если х = а ≈ 5,16, то полустанка вообще строить не надо; придется вести шоссе прямо на станцию. Так же нужно поступать и в случаях, когда расстояние а короче 5,16 км.

На этот раз мы оказываемся предусмотрительнее, нежели уравнение. Если бы мы слепо доверились уравнению, нам пришлось бы в рассматриваемом случае построить полустанок за станцией, что было бы явной нелепостью: в этом случае х > а и потому время

(а - х)/0,8,

в течение которого нужно ехать по железной дороге, отрицательно. Случай поучительный, показывающий, что при пользовании математическим орудием надо с должной осмотрительностью относиться к получаемым результатам, помня, что они могут потерять реальный смысл, если не выполнены предпосылки, на которых основывалось применение нашего математического орудия.