Два поезда

Задача

Два железнодорожных пути скрещиваются под прямым углом. К месту скрещения одновременно мчатся по этим путям два поезда: один со станции, находящейся в 40 км от скрещения, другой со станции в 50 км от того же места скрещения. Первый делает в минуту 800 м, второй - 600 м.

Через сколько минут, считая с момента отправления, паровозы были в наименьшем взаимном расстоянии? И как велико это расстояние?

Решение

Начертим схему движения поездов нашей задачи. Пусть прямые АВ и CD - скрещивающиеся пути (рис. 19). Станция В расположена в 40 км от точки скрещения О, станция D - в 50 км от нее. Предположим, что спустя х минут паровозы будут в кратчайшем взаимном расстоянии друг от друга MN = m.

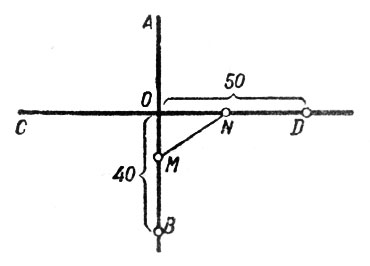
Рис. 19. Начертим схему движения поездов нашей задачи

Поезд, вышедший из В, успел к этому моменту пройти путь ВМ = 0,8x, так как за минуту он проходит 800 м = 0,8 км. Следовательно, ОМ = 40 - 0,8x. Точно так же найдем, что ОN = 50 - 0,6x. По теореме Пифагора

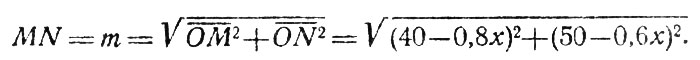
Возвысив в квадрат обе части уравнения

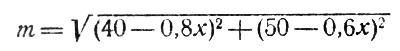
и сделав упрощения, получаем:

 х2 - 124x + 4100 - m2 = 0.

Решив это уравнение относительно х, имеем:

           ________
 x = 62 ± √m2 - 256.

Так как х - число протекших минут - не может быть мнимым, то m² - 256 должно быть величиной положительной, или в крайнем случае равняться нулю. Последнее соответствует наименьшему возможному значению m, и тогда

 m2 = 256, т. е. m = 16.

Очевидно, что m меньше 16 быть не может, иначе х становится мнимым. А если m² - 256 = 0, то х = 62.

Итак, паровозы окажутся всего ближе друг к другу через 62 мин., и взаимное их удаление тогда будет 16 км.

Определим, как они в этот момент расположены. Вычислим длину ОМ; она равна

 40 - 62 × 0,8 = -9,6.

Знак минус означает, что паровоз пройдет за скрещение на 9,6 км. Расстояние же ON равно

 50 - 62 × 0,6 = 12,8,

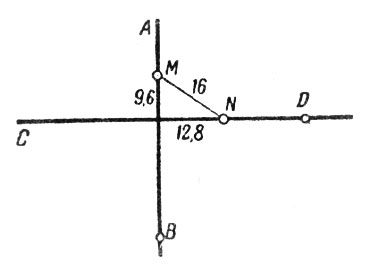
Рис. 20. Расположение паровозов

т. е. второй паровоз не дойдет до скрещения на 12,8 км. Расположение паровозов показано на рис. 20. Как видим, оно вовсе не то, какое мы представляли себе до решения задачи. Уравнение оказалось достаточно терпимым и, несмотря на неправильную схему, дало правильное решение. Нетрудно понять, откуда эта терпимость: она обусловлена алгебраическими правилами знаков.