Что больше?

Задача 1

Что больше ?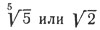

Эту и следующие задачи требуется решить, не вычисляя значения корней.

Решение

Возвысив оба выражения в 10-ю степень, получаем:

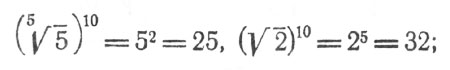
так как 32 > 25, то

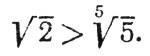
Задача 2

Что больше: ?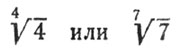

Решение

Возвысив оба выражения в 28-ю степень, получаем:

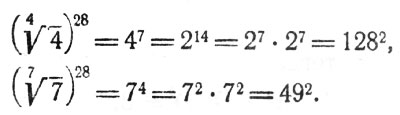
Так как 128 > 49, то и

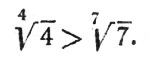
Задача 3

              _    __      _    __
 Что больше: √7 + √10 или √3 + √19?

Решение

Возвысив оба выражения в квадрат, получаем:

   _    __            __
 (√7 + √10)2 = 17 + 2√70,
   _    __            __
 (√3 + √19)2 = 22 + 2√57.

Уменьшим оба выражения на 17; у нас останется

   __         __
 2√70 и 5 + 2√57.

Возвышаем эти выражения в квадрат. Имеем:

                __
 280 и 253 + 20√57.

Отняв по 253, сравниваем

         __
 27 и 20√57.

          __                 __
 Так как √57 больше 2, то 20√57 > 40; следовательно, 

  _    __    _    __
 √3 + √19 > √7 + √10.