Пифагоровы числа

Удобный и очень точный способ, употребляемый землемерами для проведения на местности перпендикулярных линий, состоит в следующем. Пусть через точку А требуется к прямой MN провести перпендикуляр (рис. 13). Откладывают от А по направлению AM три раза какое-нибудь расстояние а. Затем завязывают на шнуре три узла, расстояния между которыми равны 4а и 5а. Приложив крайние узлы к точкам А и В, натягивают шнур за средний узел. Шнур расположится треугольником, в котором угол А - прямой.

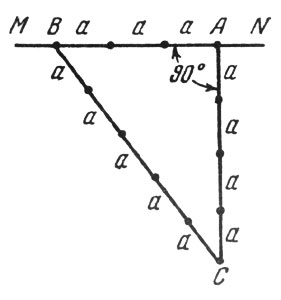
Рис. 13. Пусть через точку А требуется к прямой MN провести перпендикуляр

Этот древний способ, по-видимому, применявшийся еще тысячелетия назад строителями египетских пирамид, основан на том, что каждый треугольник, стороны которого относятся, как 3:4:5, согласно общеизвестной теореме Пифагора, - прямоугольный, так как

32 + 42 = 52.

Кроме чисел 3, 4, 5, существует, как известно, бесчисленное множество целых положительных чисел а, b, с, удовлетворяющих соотношению

а2 + b2 = с2.

Они называются пифагоровыми числами. Согласно теореме Пифагора такие числа могут служить длинами сторон некоторого прямоугольного треугольника; поэтому а и b называют "катетами", а с - "гипотенузой".

Ясно, что если а, b, с есть тройка пифагоровых чисел, то и ра, рb, рс, где р - целочисленный множитель, - пифагоровы числа. Обратно, если пифагоровы числа имеют общий множитель, то на этот общий множитель можно их все сократить, и снова получится тройка пифагоровых чисел. Поэтому будем вначале исследовать лишь тройки взаимно простых пифагоровых чисел (остальные получаются из них умножением на целочисленный множитель р).

Покажем, что в каждой из таких троек а, b, с один из "катетов" должен быть четным, а другой нечетным. Станем рассуждать "от противного". Если оба "катета" а и b четны, то четным будет число a² + b², a значит, и "гипотенуза". Это, однако, противоречит тому, что числа а, b, с не имеют общих множителей, так как три четных числа имеют общий множитель 2. Таким образом, хоть один из "катетов" а, b нечетен.

Остается еще одна возможность: оба "катета" нечетные, а "гипотенуза" четная. Нетрудно доказать, что этого не может быть. В самом деле: если "катеты" имеют вид

2х + 1 и 2у + 1,

то сумма их квадратов равна

4х2 + 4х + 1 + 4у2 + 4у + 1 = 4(х2 + х + у2 + у) + 2,

т. е. представляет собой число, которое при делении на 4 дает в остатке 2. Между тем квадрат всякого четного числа должен делиться на 4 без остатка. Значит, сумма квадратов двух нечетных чисел не может быть квадратом четного числа; иначе говоря, наши три числа - не пифагоровы.

Итак, из "катетов" а, b один четный, а другой нечетный. Поэтому число а² + b² нечетно, а значит, нечетна и "гипотенуза" с.

Предположим, для определенности, что нечетным является "катет" а, а четным b. Из равенства

а² + b² = с²

мы легко получаем:

а2 = с2 - b2 = (с + b)(с - b).

Множители с + b и с - b, стоящие в правой части, взаимно просты. Действительно, если бы эти числа имели общий простой множитель, отличный от единицы, то на этот множитель делились бы и сумма

(с + b) + (с - b) = 2с,

и разность

(с + b) - (с - b) = 2b,

и произведение

(с + b)(с - b) = а2, 

т. е. числа 2с, 2b и а имели бы общий множитель. Так как а нечетно, то этот множитель отличен от двойки, и потому этот же общий множитель имеют числа а, b, с, чего, однако, не может быть. Полученное противоречие показывает, что числа с + b и с - b взаимно просты.

Но если произведение взаимно простых чисел есть точный квадрат, то каждое из них является квадратом, т. е.

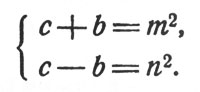
Решив эту систему, найдем:

c = (m2 + n2)/2, b = (m2 - n2)/2,

 а2 = (с + b)(с - b) = m2n2, а = mn. 

Итак, рассматриваемые пифагоровы числа имеют вид

a = mn, b = (m2 - n2)/2, с = (m2 + n2)/2.

где m и n - некоторые взаимно простые нечетные числа. Читатель легко может убедиться и в обратном: при любых нечетных тип написанные формулы дают три пифагоровых числа а, b, с.

Вот несколько троек пифагоровых чисел, получаемых при различных тип:

при m =  3, n = 1   32 +  42 =  52
при m =  5, n = 1   52 + 122 = 132
при m =  7, n = 1   72 + 242 = 252
при m =  9, n = 1   92 + 402 = 412
при m = 11, n = 1  112 + 602 = 612
при m = 13, n = 1  132 + 842 = 852
при m =  5, n = 3  152 +  82 = 172
при m =  7, n = 3  212 + 202 = 292
при m = 11, n = 3  332 + 562 = 652
при m = 13, n = 3  392 + 802 = 892
при m =  7, n = 5  352 + 122 = 372
при m =  9, n = 5  452 + 282 = 532
при m = 11, n = 5  552 + 482 = 732
при m = 13, n = 5  652 + 722 = 972
при m =  9, n = 7  632 + 162 = 652
при m = 11, n = 7  772 + 362 = 852

(Все остальные тройки пифагоровых чисел или имеют общие множители, или содержат числа, большие ста.)

Пифагоровы числа обладают вообще рядом любопытных особенностей, которые мы перечисляем далее без доказательств:

1. Один из "катетов" должен быть кратным трем.
2. Один из "катетов" должен быть кратным четырем.
3. Одно из пифагоровых чисел должно быть кратно пяти.

Читатель может удостовериться в наличии этих свойств, просматривая приведенные выше примеры групп пифагоровых чисел.