Неопределенное уравнение третьей степени

Сумма кубов трех целых чисел может быть кубом четвертого числа. Например, 3³ + 4³ + 5³ = 6³.

Это означает, между прочим, что куб, ребро которого равно 6 см, равновелик сумме трех кубов, ребра которых равны 3 см, 4 см и 5 см (рис. 14), - соотношение, по преданию, весьма занимавшее Платона.

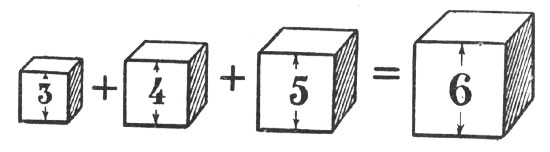
Рис. 14. Куб, ребро которого равно 6 см, равновелик сумме трех кубов, ребра которых равны 3 см, 4 см и 5 см

Попытаемся найти другие соотношения такого же рода, т. е. поставим перед собой такую задачу: найти решения уравнения x3+y3+z3=u3. Удобнее, однако, обозначить неизвестное и через -t. Тогда уравнение будет иметь более простой вид

x3 + y3 + z3 + t3 = 0.

Рассмотрим прием, позволяющий найти бесчисленное множество решений этого уравнения в целых (положительных и отрицательных) числах. Пусть а, b, с, d и α, β, γ, δ - две четверки чисел, удовлетворяющих уравнению. Прибавим к числам первой четверки числа второй четверки, умноженные на некоторое число k, и постараемся подобрать число k так, чтобы полученные числа

a + kα, b + kβ, c + kγ, d + kδ

также удовлетворяли нашему уравнению. Иначе говоря, подберем k таким образом, чтобы было выполнено равенство

(a + kα)3 + (b + kβ)3 + (c + kγ)3 + (d + kδ)3 = 0.

Раскрыв скобки и вспоминая, что четверки a, b,c,d и α, β, γ, δ удовлетворяют нашему уравнению, т. е. имеют место равенства

a3 + b3 + c3 + d3 = 0, α3 + β3 + γ3 + δ3 = 0,

мы получим:

 3a2kα + 3ak2α2 + 3b2kβ + 3bk2β2 + 3c2kγ + 3ck2γ2 + 3d2kδ + 3dk2δ2 = 0 

или

3k[(a2a + b2β + c2γ + d2δ) + k(aα2 + bβ2 + cγ2 + dδ2)] = 0. 

Произведение может обращаться в нуль только в том случае, когда обращается в нуль хотя бы один из его множителей. Приравнивая каждый из множителей нулю, мы получаем два значения для k. Первое значение, k = 0, нас не интересует: оно означает, что если к числам а, Ь, с, d ничего не прибавлять, то полученные числа удовлетворяют нашему уравнению. Поэтому мы возьмем лишь второе значение для k:

k = - (a2α + b2β + c2γ + d2δ

Итак, зная две четверки чисел, удовлетворяющих исходному уравнению, можно найти новую четверку: для этого нужно к числам первой четверки прибавить числа второй четверки, умноженные на k, где k имеет написанное выше значение.

Для того чтобы применить этот прием, надо знать две четверки чисел, удовлетворяющих исходному уравнению. Одну такую четверку (3, 4, 5,-6) мы уже знаем. Где взять еще одну четверку? Выход из положения найти очень просто: в качестве второй четверки можно взять числа r, -r, s, -s, которые, очевидно, удовлетворяют исходному уравнению. Иначе говоря, положим:

а = 3, b = 4, с = 5, d = -6, 
α = r, β = - r, γ = s, δ = - s.

Тогда для k мы получим, как легко видеть, следующее значение:

k = -(-7r - 11s)/ (7r2 - s2) = (7r + 11s)/(7r2 - s2),

а числа a + kα, b + kβ, c + kγ, d + kδ будут соответственно равны

(28r2 + 11rs - 3s2)/(7r2 - s2), (21r2 - 11rs - 4s2)/(7r2 - s2), 

(35r2 + 7rs + 6s2)/(7r2 - s2), (-42r2 - 7rs - 5s2)/(7r2 - s2).

Согласно сказанному выше эти четыре выражения удовлетворяют исходному уравнению

x3 + y3 + z3 + t3 = 0.

Так как все эти выражения имеют одинаковый знаменатель, то его можно отбросить (т. е. числители этих дробей также удовлетворяют рассматриваемому уравнению). Итак, написанному уравнению удовлетворяют (при любых r и s) следующие числа:

x =  28r2 + 11rs - 3s2, 
у =  21r2 - 11rs - 4s2, 
z =  35r2 +  7rs + 6s2, 
t = -42r2 -  7rs - 5s2,

в чем, конечно, можно убедиться и непосредственно, возведя эти выражения в куб и сложив. Придавая r и s различные целые значения, мы можем получить целый ряд целочисленных решений нашего уравнения. Если при этом получающиеся числа будут иметь общий множитель, то на него можно эти числа разделить. Например, при r = 1, s = 1 получаем для х, y, z, t следующие значения: 36, 6, 48, -54, или, после сокращения на 6, значения 6, 1, 8, -9. Таким образом,

63 + 13 + 83 = 93.

Вот еще ряд равенств того же типа (получающихся после сокращения на общий множитель):

при r = 1, s = 2   383 +  733 = 173 +  763,
при r = 1, s = 3   173 +  553 = 243 +  543,
при r = 1, s = 5    43 + 1103 = 673 + 1013,
при r = 1, s = 4    83 +  533 = 293 +  503,
при r = 1, s = -1   73 +  143 + 173 =  203,
при r = 1, s = -2   23 +  163 =  93 +  153,
при r = 2, s = -1  293 +  343 + 443 =  533.

Заметим, что если в исходной четверке, 3, 4, 5, -6 или в одной из вновь полученных четверок поменять числа местами и применить тот же прием, то получим новую серию решений. Например, взяв четверку 3, 5, 4, -6 (т. е. положив a = 3, b = 5, с = 4, d = -6), мы получим для х, y, z, t значения:

х =  20r2 + 10rs - 3s2, 
y =  12r2 - 10rs - 5s2, 
z =  16r2 +  8rs + 6s2, 
t = -24r2 -  8rs - 4s2.

Отсюда при различных r и s получаем ряд новых соотношений:

при r = 1, s = 1    93 +  103 =   13 +  123,
при r = 1, s = 3   233 +  943 =  633 +  843,
при r = 1, s = 5    53 + 1633 + 1643 = 2063,
при r = 1, s = 6    73 +  543 +  573 =  703,
при r = 2, s = 1   233 +  973 +  863 = 1163,
при r = 1, s = -3   33 +  363 +  373 =  463 и т. д.

Таким путем можно получить бесчисленное множество решений рассматриваемого уравнения.