Две жестянки кофе

Задача

Две жестянки, наполненные кофе, имеют одинаковую форму и сделаны из одинаковой жести. Первая весит 2 кг и имеет в высоту 12 см\ вторая весит 1 кг и имеет в высоту 9,5 см. Каков чистый вес кофе в жестянках?

Решение

Обозначим вес содержимого большей жестянки через х, меньшей - через у. Вес самих жестянок обозначим соответственно через z и t Имеем уравнения

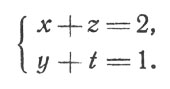
Так как веса содержимого полных жестянок относятся, как их объемы, т. е. как кубы их высот^*,то

x/y = 123/9,53 ≈ 2,02 или х = 2,02у.

^* (Пропорцией этой позволительно пользоваться лишь в том случае, когда стенки жестянок не слишком толсты (так как наружная и внутренняя поверхности жестянок, строго говоря, не подобны и, кроме того, высота внутренней полости банки, строго говоря, отличается от высоты самой банки).)

Веса же пустых жестянок относятся, как их полные поверхности, т. е. как квадраты их высот. Поэтому

z/t = 122/9,52 ≈ 1,60 или z = 1,60t.

Подставив значения х и z в первое уравнение, получаем систему

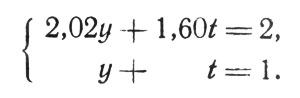
Решив ее, узнаем:

у = 20/21 = 0,95,  t = 0,05.

И следовательно,

x = 1,92, z = 0,08.

Вес кофе без упаковки: в большей жестянке 1,92 кг, в меньшей - 0,94 кг.