Пароход и плоты

Задача

Из города А в город В, расположенный ниже по течению реки, пароход шел (без остановок) 5 часов. Обратно, против течения, он шел (двигаясь с той же собственной скоростью и также не останавливаясь) 7 часов. Сколько часов идут из А в В плоты (плоты движутся со скоростью течения реки)?

Решение

Обозначим через х время (в часах), нужное пароходу для того, чтобы пройти расстояние от A до В в стоячей воде (т. е. при движении с собственной скоростью), а через у - время движения плотов. Тогда за час пароход проходит 1/x расстояния АВ, а плоты (течение) 1/y этого расстояния. Поэтому вниз по

реке пароход проходит за час 1/x + 1/y расстояния АВ, а вверх (против течения) 1/x - 1/y. Мы же знаем из условия задачи, что вниз по реке пароход проходит за час 1/5 расстояния, а вверх 1/7. Получаем систему

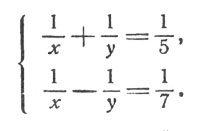
Заметим, что для решения этой системы не следует освобождаться от знаменателей: нужно просто вычесть из первого уравнения второе. В результате мы получим:

2/y = 2/35,

откуда y = 35. Плоты идут из А в В 35 часов.