Перестановка часовых стрелок

Задача

Биограф и друг известного физика А. Эйнштейна А. Мошковский, желая однажды развлечь своего приятеля во время болезни, предложил ему следующую задачу (рис. 9):

"Возьмем, - сказал Мошковский, - положение стрелок в 12 часов. Если бы в этом положении большая и малая стрелки обменялись местами, они дали бы все же правильные показания. Но в другие моменты, - например, в 6 часов, взаимный обмен стрелок привел бы к абсурду, к положению, какого на правильно идущих часах быть не может: минутная стрелка не может стоять на 6, когда часовая показывает 12. Возникает вопрос: когда и как часто стрелки часов занимают такие положения, что замена одной другою дает новое положение, тоже возможное на правильных часах?

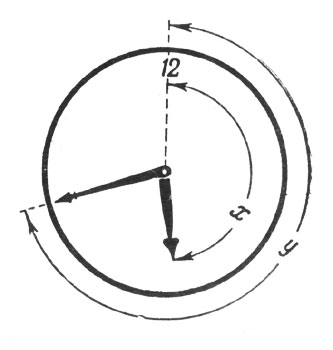
Рис. 9. Задача для Эйнштейна

- Да, - ответил Эйнштейн, - это вполне подходящая задача для человека, вынужденного из-за болезни оставаться в постели: достаточно интересная и не слишком легкая. Боюсь только, что развлечение продлится недолго: я уже напал на путь к решению.

И приподнявшись на постели, он несколькими штрихами набросал на бумаге схему, изображающую условие задачи. Для решения ему понадобилось не больше времени, чем мне на формулировку задачи..."

Как же решается эта задача?

Решение

Будем измерять расстояния стрелок по кругу циферблата от точки, где стоит цифра 12, в 60-х долях окружности.

Пусть одно из требуемых положений стрелок наблюдалось тогда, когда часовая стрелка отошла от цифры 12 на х делений, а минутная - на у делений. Так как часовая стрелка проходит 60 делений за 12 часов, т. е. 5 делений в час, то х делений она прошла за x/5 часов. Иначе говоря, после того как часы показывали 12, прошло x/5 часов. Минутная стрелка прошла у делений за у минут, т. е. за y/60 часов. Иначе говоря, цифру 12 минутная стрелка прошла y/60 часов тому назад, или через

x/5 - y/60

часов после того, как обе стрелки были на двенадцати. Это число является целым (от нуля до 11), так как оно показывает, сколько полных часов прошло после двенадцати.

Когда стрелки обменяются местами, мы найдем аналогично, что с двенадцати часов до времени, показываемого стрелками, прошло

y/5 - x/60

полных часов. Это число также является целым (от нуля до 11).

Имеем систему уравнений

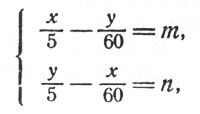
где m и n - целые числа, которые могут меняться от 0 до 11. Из этой системы находим:

 x = 60(12m + n)/143,
 y = 60(12n + m)/143.

Давая тип значения от 0 до 11, мы определим все требуемые положения стрелок. Так как каждое из 12 значений m можно сопоставлять с каждым из 12 значений n, то, казалось бы, число всех решений равно 12 × 12 = 144. Но в действительности оно равно 143, потому что при m = 0, n = 0 и при m = 11, n = 11 получается одно и то же положение стрелок.

При m = 11, n = 11 имеем:

x = 60, y = 60,

т. е. часы показывают 12, как и в случае m = 0, n = 0.

Всех возможных положений мы рассматривать не станем; возьмем лишь два примера.

Первый пример:

                  m = 1, n = 1; 

 x = (60 × 13)/143 = 5 5/11,  y = 5 5/11,

т. е. часы показывают 1 час 5 5/11 мин.; в этот момент стрелки совмещаются; их, конечно, можно обменять местами (как и при всех других совмещениях стрелок).

Второй пример:

                                     m = 8, n = 5; 

 х = 60(5 + 12 × 8)/143 ≈ 42,38,  y = 90(8 + 12 × 5)/143 ≈ 28,53.

Соответствующие моменты: 8 час. 28,53 мин. и 5 час. 42,38 мин.

Число решений мы знаем: 143. Чтобы найти все точки циферблата, которые дают требуемые положения стрелок, надо окружность циферблата разделить на 143 равные части: получим 143 точки, являющиеся искомыми. В промежуточных точках требуемые положения стрелок невозможны.