Птицы у реки

Задача

У одного арабского математика XI века находим следующую задачу.

На обоих берегах реки растет по пальме, одна против другой. Высота одной - 30 локтей, другой - 20 локтей; расстояние между их основаниями - 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами; они кинулись к ней разом и достигли ее одновременно.

Рис. 4. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами; они кинулись к ней разом и достигли ее одновременно

На каком расстоянии от основания более высокой пальмы появилась рыба?

Решение

Из схематического чертежа (рис. 5), пользуясь теоремой Пифагора, устанавливаем:

АВ2 = 302 + х2,  AС2 = 202 + (50 - х)2.

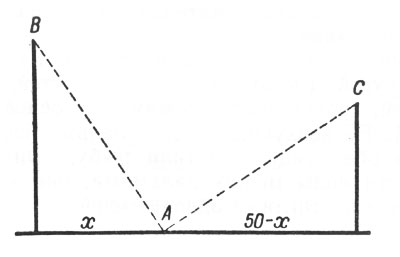
Рис. 5. Схематический чертеж

Но АВ = АС, так как обе птицы пролетели эти расстояния в одинаковое время. Поэтому

302 + x2 = 202 + (50 - х)2.

Раскрыв скобки и сделав упрощения, получаем уравнение первой степени 100x = 2000, откуда x = 20.

Рыба появилась в 20 локтях от той пальмы, высота которой 30 локтей.