
4. Деление угла на три равные части, пользуясь новой улиткой
Для построения кривой трисекции угла может быть использована схема, приведенная на рисунке 37. На ней 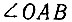 - заданный, а
- заданный, а 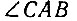 равен его третьей части. На наклонной стороне заданного угла OAB взята произвольная точка O и радиусом OA проведена окружность,
равен его третьей части. На наклонной стороне заданного угла OAB взята произвольная точка O и радиусом OA проведена окружность,
которая пересекает сторону угла OAB в точке D. Проведя через эту точку радиус OD и продолжая его до пересечения с прямой AB - второй стороной заданного угла OAB,- получим 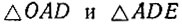 - оба равнобедренные. Докажем это.
- оба равнобедренные. Докажем это.
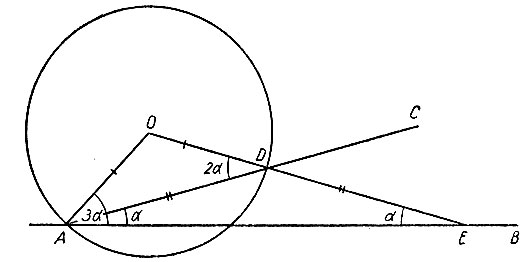
Рис. 37
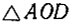
- равнобедренный, так как 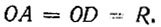 Следовательно,
Следовательно, 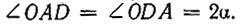 Но
Но 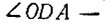 - внешний относительно
- внешний относительно 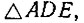 поэтому
поэтому
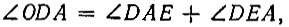
или
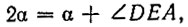
откуда 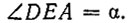
Следовательно,  - равнобедренный и AD = DE.
- равнобедренный и AD = DE.
Отсюда получаем способ деления угла на три равные части. Для этого надо из произвольной точки O, выбранной на стороне заданного угла, провести радиусом OA окружность, а затем из вершины A заданного угла провести прямую AD так, чтобы, соединив точку D с центром окружности O и продолжив полученную прямую OD до пересечения со стороной AB, получить DE = AD. На рисунке 38 показано, как найти положение прямой AD, удовлетворяющее этому условию.
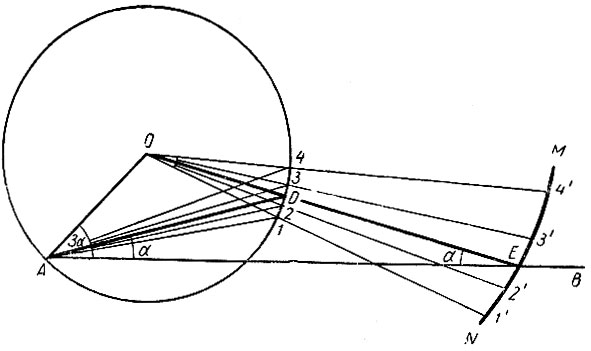
Рис. 38
Из вершины A заданного угла проводим несколько прямых, пересекающих окружность в точках 1, 2, 3 и 4. Эти точки соединяем с центром окружности, продолжаем полученные радиусы за окружность и на продолжении каждого радиуса откладываем отрезок, равный расстоянию конца радиуса от вершины A заданного угла. Таким образом, нами получены точки 1', 2', 3' и 4', которые соединяем плавной кривой MN. Точку пересечения этой кривой со стороной AB заданного угла OAB соединяем с центром окружности O. Эта прямая OE пересечет окружность в точке D, которую соединяем с вершиной А заданного угла. Так как согласно нашему построению AD = DE, то прямая AD и является искомой.
Чтобы избежать необходимости строить указанным выше способом кривую MN для каждого угла, который требуется разделить на три равные части, на рисунке 39 дается построение полной кривой. Способ построения ее следующий. Точка P, центр окружности, принята за полюс, сама окружность принята за базис, а отрезки, откладываемые на продолжениях радиусов, в отличие от кривых конхоид не равны друг другу, а изменяются по следующему определенному закону. Принимаем точку O на окружности за второй полюс и из него проводим лучи до концов радиусов. Получаем отрезки O1, O2, O3, O4 и т. д. Каждый из этих отрезков откладываем на продолжении своего радиуса, т. е. откладываем 11' = O1, 22' = O2, 33' = O3, 44' = O4 и т. д. Полученные точки 1', 2', 3', 4' и т. д. соединяем плавной кривой.
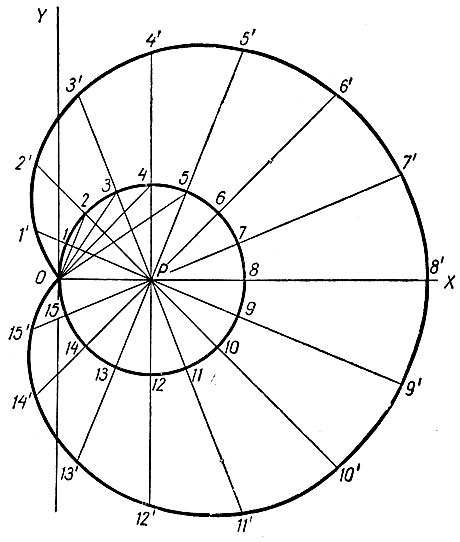
Рис. 39
Как видим, откладываемые отрезки сперва увеличиваются от нуля до длины, равной диаметру окружности, а потом уменьшаются снова до нуля. Полученная кривая по своему виду напоминает улитку Паскаля, поэтому дальше называем ее новой улиткой.
На рисунке 40 построена номограмма для трисекции углов при помощи такой улитки. Номограмма состоит из половины новой улитки и полуокружности. Точка O является вершиной заданного угла. Из рисунка 40 видно, что для нахождения третьей части заданного угла AOP достаточно точку A соединить с точкой P, тогда 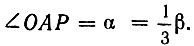 Если точку B, полученную при пересечении прямой AP с окружностью, соединить с точкой O, то получим
Если точку B, полученную при пересечении прямой AP с окружностью, соединить с точкой O, то получим 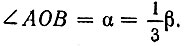 Докажем это.
Докажем это.
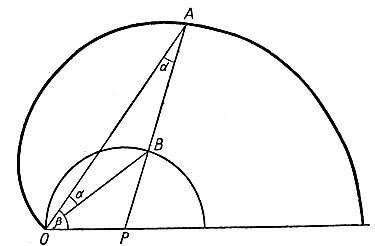
Рис. 40
По способу построения этой улитки имеем, что OB = BA, следовательно, 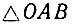 - равнобедренный и
- равнобедренный и 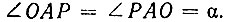 Но
Но 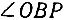 - внешний относительно
- внешний относительно 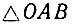 , поэтому
, поэтому 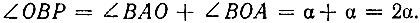 В свою очередь
В свою очередь 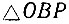 - тоже равнобедренный, так как OP = PB = R, следовательно,
- тоже равнобедренный, так как OP = PB = R, следовательно, 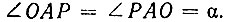 а
а 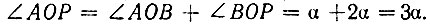 Таким образом, проводя прямую OB, отсекаем от заданного угла его третью часть. Пользуясь этой номограммой, можно произвести трисекцию любого угла от 0° до 135°.
Таким образом, проводя прямую OB, отсекаем от заданного угла его третью часть. Пользуясь этой номограммой, можно произвести трисекцию любого угла от 0° до 135°.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'