5. Номограмма для трисекции острых и тупых (до 180°) углов

Все приведенные выше способы деления угла на три равные части в большинстве своем давали решение только для острых углов и лишь, пользуясь новой улиткой, представляется возможным разделить на три равные части и тупой угол, если он не более 135°.

Ниже приводим построение кривой трисекции угла, пользуясь которой можно разделить на три равные части как острый, так и тупой (до 180°) углы.

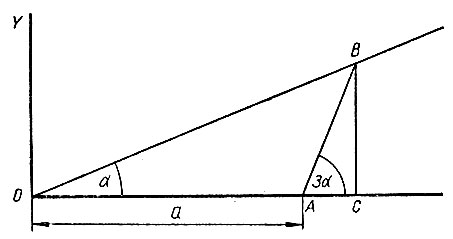
Рис. 41

На рисунке 41 дана схема построения такой кривой. На ней 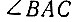- заданный, т. е. угол, который требуется обоих углов - искомая точка нашей кривой трисекции углов. Если для каждого угла с вершиной в точке O будем строить соответственно угол, в три раза больший его, с вершиной в точке A, то наклонные прямые будут пересекаться для каждой комбинации углов в другой точке, причем, если 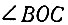будем увеличивать, то точка B будет перемещаться влево, а если уменьшать, то вправо.

На рисунке 42 показано построение кривой трисекции угла по описанному методу. Точка А является вершиной изменяющегося искомого угла α, а точка B - вершиной разделить на три равные части, а 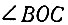равен одной трети заданного, т. е. искомый. Горизонтальные стороны этих углов совпадают. Расстояние между вершинами этих углов OA = α. Точка В - пересечение наклонных сторон соответствующего заданного угла 3α. Нумерация точек на полуокружности с центром в точке B и нумерация точек на дуге окружности с центром в точке A соответствующая. Радиусы полуокружности и дуги одинаковые. Расстояние AB = 2R. Построение точек кривой трисекции ясно из рисунка 42. Нумерация построенных точек соответствует нумерации точек на полуокружности и на дуге. Выведем уравнение построенной кривой трисекции угла.

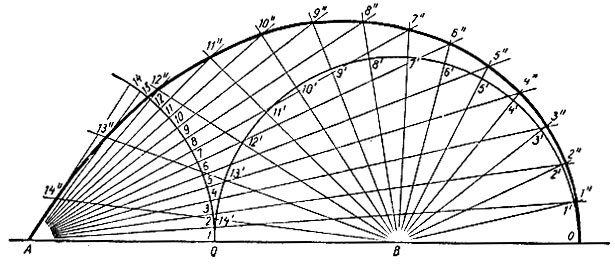
Рис. 42

Из схемы на рисунке 41 видно, что координаты точки B связаны следующими зависимостями:

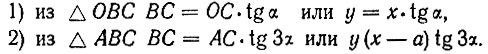
Следовательно,

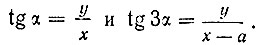
Выведем зависимость между tg α и tg 3α.

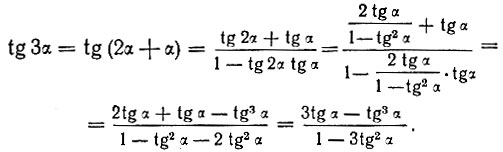
Подставляя в выведенную нами зависимость значения tg 3α и tg α, получим:

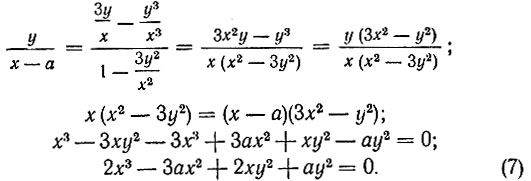
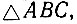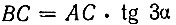Это будет уравнение кривой трисекции угла для той ее части, которая расположена вправо от точки A (см. рис. 41). Для части, которая расположена влево от этой точки, будем иметь из что или 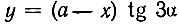и соответственно:

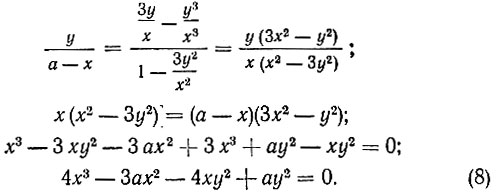
Очевидно, что при x = a уравнения (7) и (8) должны быть тождественны.

Для уравнения (7) при x = a имеем:

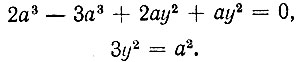
Для уравнения (8) при x = a имеем:

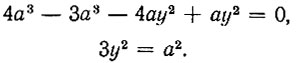
Как видим, ордината у в точке сопряжения обеих кривых трисекции угла совпадает.

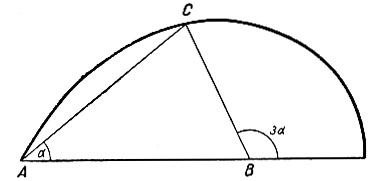
Рис. 43

На рисунке 43 дана номограмма трисекции острого и тупого (до 180°) углов, пользуясь построенной кривой. На ней точка B - вершина заданного угла, а точка A - вершина искомого угла. Способ пользования виден из приведенного примера.