3. Деление угла на три равные части, пользуясь улиткой Паскаля

Рассмотрим приведенную раньше схему деления угла на три равные части по Архимеду. Из нее видим, что из вершины заданного угла проводится произвольным радиусом окружность, а затем из точки пересечения окружности с наклонной стороной заданного угла проводят прямую DA так, чтобы отрезок AB = R. Для этого, очевидно, достаточно провести через точку D несколько лучей и на каждом из них отложить, начиная от точки пересечения луча с окружностью, отрезок, равный R, и полученные точки соединить кривой, как это сделано на рисунке 34. Пересечение этой кривой EF с продолжением стороны OC заданного угла и даст искомую точку A. Легко сообразить, что полученный

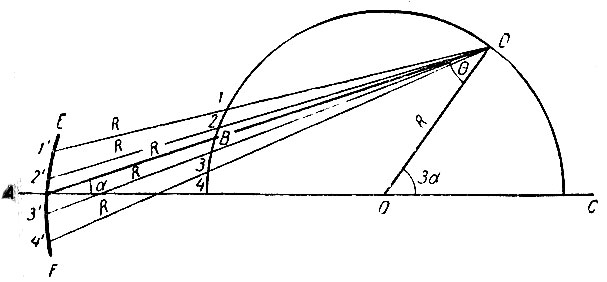
Рис. 34

По методу построения кривой EF видим, что эта кривая представляет собой часть круговой конхоиды (улитки Паскаля). Базисом ее является круг радиуса R, полюсом точка P, расположенная на окружности. На лучах, проводимых из полюса, от точек их пересечения с базисом откладываются одинаковые отрезки, равные радиусу круга R. Уравнение такой улитки Паскаля в прямоугольных координатах, если за начало координат принять полюс, будет

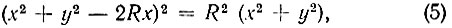
а в полярных координатах

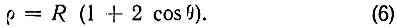
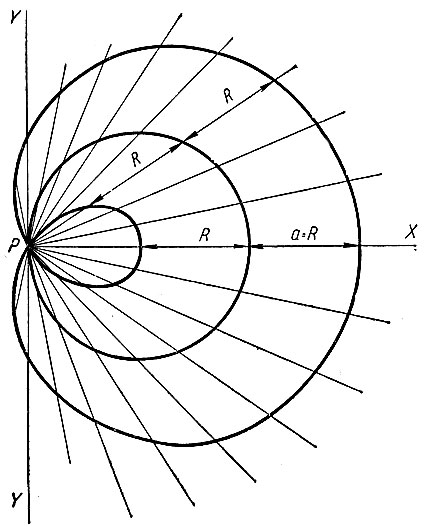
Рис. 35

Следовательно, улитка Паскаля, в которой откладываемый отрезок равен радиусу круга, принятого за базис, будет представлять собой и кривую трисекции угла.

На рисунке 35 дано построение такой улитки Паскаля. Так как откладываемый отрезок менее диаметра круга, то улитка Паскаля имеет петлю, показанную на рисунке 35.

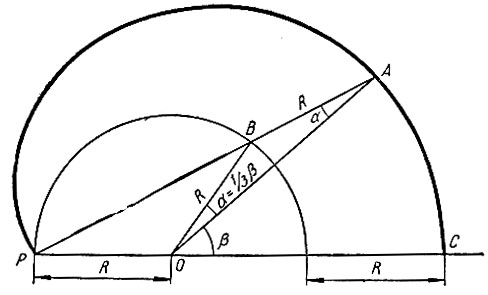
Рис. 36

Номограмма для трисекции угла при помощи улитки Паскаля дана на рисунке 36. Она состоит из верхней ветви улитки (без петли) и полуокружности. Вершиной заданного угла является центр полуокружности. Для нахождения третьей части заданного угла AOC достаточно соединить точку A, полученную от пересечения стороны OA угла AOC с улиткой Паскаля, с полюсом P. Полученный 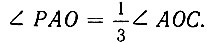Если точку B пересечения прямой PA с кругом соединить с центром круга, то полученный 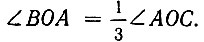Докажем это. Из построения на номограмме видим, что 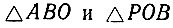- равнобедренные, так как

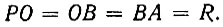
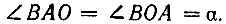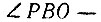Следовательно, Но внешний относительно 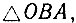поэтому 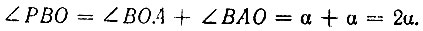Из 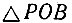имеем: 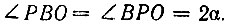Заданный угол AOC - внешний относительно 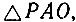поэтому имеем: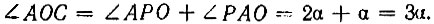

Следовательно,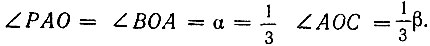

Если для трисекции углов, пользуясь конхоидой прямой Никомеда, требуется для каждого заданного угла строить свою конхоиду, то при использовании улитки Паскаля для тех же целей достаточно построить такую улитку один раз и она может быть использована для трисекции любого острого угла.