2. Внутренние и внешние кривые трисекции углов первой четверти окружности

Метод нахождения геометрических мест точек, удовлетворяющих какому-либо условию, в настоящее время широко применяется как в номографии, так и при решении геометрических задач на построение. Пользуясь им, удалось построить несколько кривых трисекции угла. Приведем описание двух наиболее простых построений этих кривых.

На рисунке 27 показана схема построения внутренних кривых трисекции острых углов. На этом рисунке дана четверть окружности, положение радиуса OC, определяющего заданный угол COA = 3α, положение радиуса OD, определяющего искомый угол DOA = α, и положение радиуса OE, определяющего угол EOA = 2α.

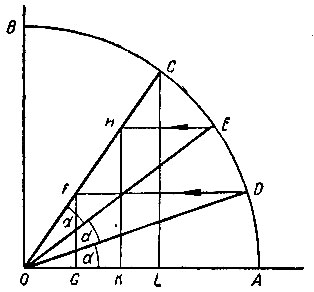
Рис. 27

Если через точку D провести прямую 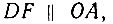то, очевидно, зная положение точки F на радиусе OC, легко решить обратную задачу, т. е. найти положение точки D на окружности, а соединив ее с центром окружности, построим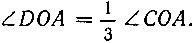

Если для каждого угла найдем положение радиуса, образующего угол 3α, и на нем отметим положение точки F, как это сделано на рисунке 27, то, соединяя все эти точки F плавной кривой, получим геометрическое место точек, обладающих одним и тем же свойством; а именно: если провести радиус, отсекающий заданный угол, и точку пересечения этого радиуса с построенной кривой перенести параллельно радиусу OA на окружность и полученную точку соединить с центром окружности, то построенный таким способом угол равен 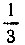заданного угла.

На рисунке 28 показано построение кривой CD, которая отвечает геометрическому месту точек F рисунка 27.

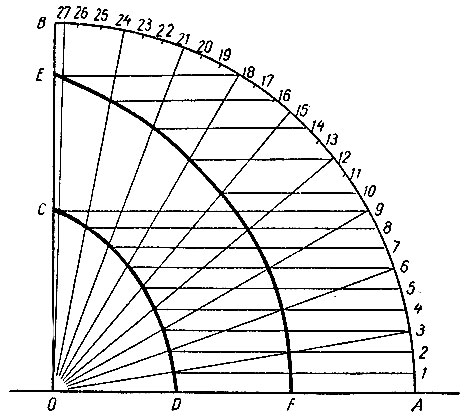
Рис. 28

На схеме, приведенной на рисунке 27, показано также положение радиуса OE, определяющего ∠EOA = 2α. Если через точку E провести 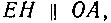то получим в пересечении с радиусом точку H. Очевидно, зная положение точки H, легко найти положение точки E на окружности, а следовательно, построить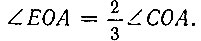

Геометрическое место точек H даст вторую внутреннюю кривую трисекции острого угла. На рисунке 28 показано так же, как построена кривая EF, отвечающая этому геометрическому месту точек.

Построение обеих внутренних кривых трисекции угла не сложнее построения квадратрисы Гиппия, но способ пользования ими проще и отчетливее, как это видно из номограммы, приведенной на рисунке 29. На ней даны обе построенные нами внутренние кривые трисекций угла и четверть соответствующей окружности. Приведенный на ней пример использования номограммы полагаем не нуждается в пояснении.

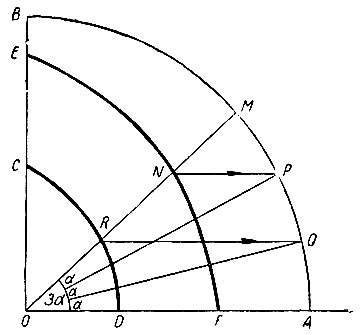
Рис. 29

Выведем уравнения обеих кривых в полярных координатах^*. Из рисунка 27 имеем, что откуда

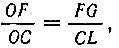
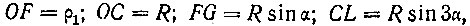
следовательно,

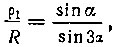
или

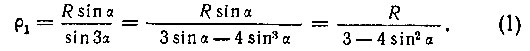
^* (С полярными координатами учащиеся могут познакомиться по книге Н. В. Ефимова "Краткий курс аналитической геометрии", ГИТТЛ, 1956, стр. 16-18.)

Это уравнение первой (более близкой к центру окружности) внутренней кривой трисекции угла в полярных координатах, где угол α - третья часть заданного угла.

Из рисунка 27 имеем также, что 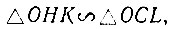откуда

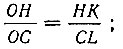
но

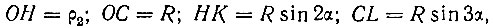
следовательно,

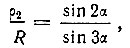
или

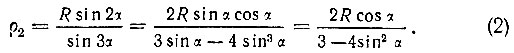
Полученное уравнение (2) будет уравнением второй внутренней кривой трисекции угла в полярных координатах, где угол α - третья часть заданного угла.

Применяя весьма схожий метод, можно построить две наружные кривые трисекции угла. На рисунке 30 дана схема такого построения.

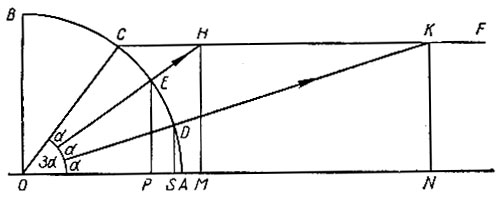
Рис. 30

Она отличается от схемы на рисунке 27 тем, что в ней проводят горизонтальную прямую CF через точку C, являющуюся концом радиуса, отвечающего заданному углу COA, а радиусы OE и OD, отвечающие углам 2α и α, продолжают до пересечения в точках H и K с прямой CF. Очевидно, что если знать положение точек H и K на прямой CF, то провести радиусы OE и OD не представляет труда. Следовательно, и в данном случае задача сводится к построению геометрического места точек H и геометрического места точек K.

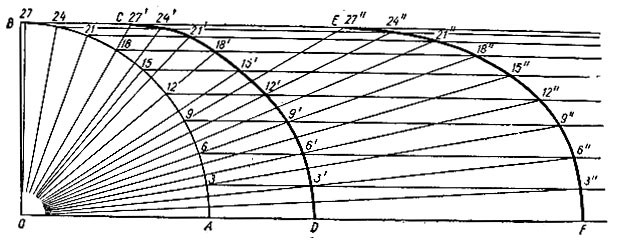
Рис. 31

Это построение показано на рисунке 31, где кривая CD представляет геометрическое место точек пересечения продолжении радиусов, отвечающих 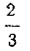заданного угла, с горизонталями, проведенными через концы радиусов заданных углов, а кривая EF - геометрическое место точек пересечения продолжений радиусов, отвечающих 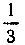заданного угла, с теми же горизонталями.

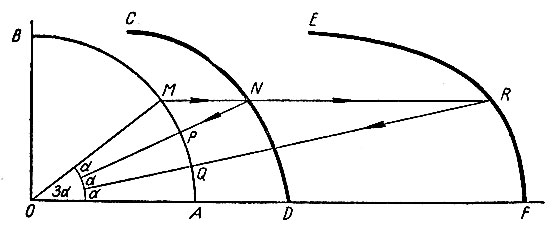
Рис. 32

На рисунке 32 дана еще одна номограмма трисекции угла, для которой использованы обе внешние кривые, построенные на рисунке 31. Способ пользования номограммой весьма прост и ясен из приведенного на ней примера. Выведем уравнения обеих внешних кривых трисекций угла в полярных координатах.

Из рисунка 30 имеем, что откуда

но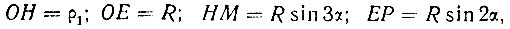

следовательно,

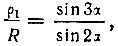
откуда

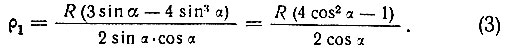
Это уравнение первой (более близкой к центру окружности) внешней кривой трисекции угла в полярных координатах, где угол α - третья часть заданного угла.

Из той же схемы на рисунке 30 имеем, что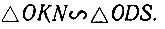

Откуда

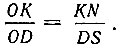
Но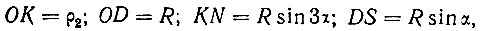

следовательно,

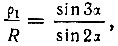
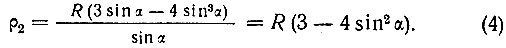
Полученное уравнение (4) будет уравнением второй внешней кривой трисекции угла в полярных координатах, где угол α - третья часть заданного угла.

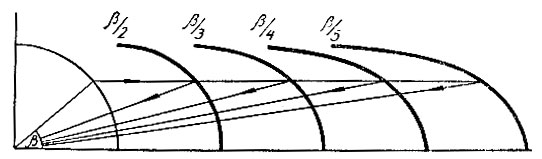
Рис. 33

Очевидно, пользуясь подобными методами, можно построить номограммы для деления любого острого угла на две, три, четыре и т. д. равные части. Подобная номограмма дана на рисунке 33. На ней, кроме четверти окружности, имеются четыре кривые. Первая, обозначенная 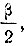служит для деления угла пополам; вторая, обозначенная -

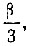для деления угла на'три равные части; третья, обозначенная 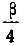- для деления угла на четыре равные части и четвертая, обозначенная 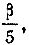- для деления угла на пять равных частей. Способ пользования номограммой виден из приведенного на ней примера.