1. Номограмма для трисекции острого угла, построенная по формуле

Приводим метод построения номограммы формулы,

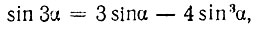
не прибегая к каким-либо вычислениям и используя лишь циркуль и линейку без делений.

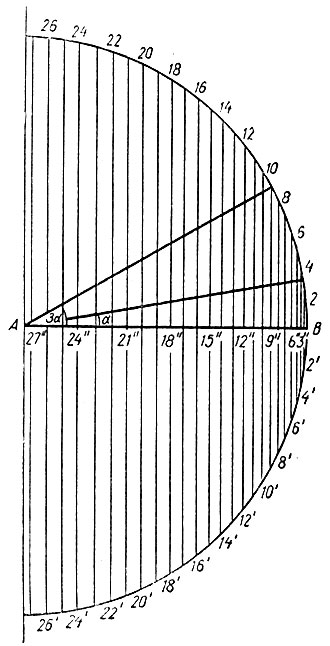
Рис. 24

Для того чтобы избежать необходимость вычислять по тригонометрическим таблицам значения sin α и sin 3α, на рисунке 24 построен график синусов углов. Для этого по окружности верхнего квадранта от точки В отложены 27 равных дуг и точки их концов пронумерованы от 1 до 27. Очевидно, что перпендикуляры из этих точек на радиус AB равны синусам соответствующих центральных углов. Так как опускать перпендикуляры из всех точек на радиус AB требует значительных геометрических построений, то на том же рисунке построен и нижний квадрант окружности и на нем отложены от той же точки B те же 27 равных дуг и точки их концов также пронумерованы от 1 до 27, но со значком прим. Соединяя одноименные точки верхнего и нижнего квадранта, избавляемся от необходимости опускать перпендикуляры - на радиус AB. Пользуясь рисунком 24, можно без всяких вычислений для заданного угла α и соответствующего ему угла За найти величины отрезков, отвечающие их синусам, хотя значения эти являются величинами несоизмеримыми.

На рисунке 25 дана кривая формулы:

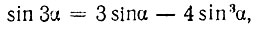
Построение выполнено в следующей последовательности. Тем же радиусом AB, что и на рисунке 24, на рисунке 25 построена четверть окружности. Горизонтальная ось принята за ось sin α, а вертикальная - за ось sin 3α. За начало координат принята точка A. По горизонтальной оси от точки А отложены отрезки, равные синусам углов, которым отвечают точки от 1 до 9 на рисунке 24. Нумерация этих точек сохранена та же. От каждой из полученных точек отложены вверх по перпендикулярам к радиусу AB отрезки, равные синусам соответствующих тройных углов, что отвечает номерам точек, кратных трем (3, 6, 9 и т. д.). На рисунке 25 этим точкам присвоена такая же нумерация. Следовательно, кривая AC, построенная по точкам на рисунке 25, представляет собой кривую зависимости sin 3α от sin α, т. е. кривую формулы

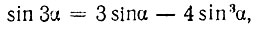
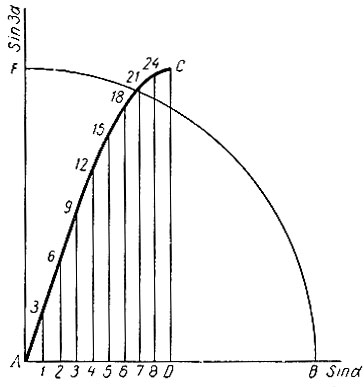
Рис. 25

Для того чтобы использовать кривую AC для деления любого острого угла на три равные части, на рисунке 26 построена номограмма, на которой, кроме кривой AC и квадранта окружности FB, еще проведена прямая AE под углом 45° к горизонтальной оси AB. Эта прямая нужна для того, чтобы горизонтальный отрезок по оси AB, отвечающий значению sin α, преобразовать в равный ему вертикальный отрезок и найти соответствующую ему точку на квадранте FB окружности.

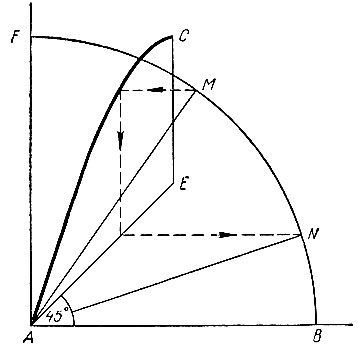
Рис. 26

На номограмме дано построение для следующего примера: требуется найти третью часть угла MAB. Из точки M проводим горизонталь до кривой AC, затем вертикаль до прямой AE и далее горизонталь до пересечения с окружностью FB в точке N, которую соединяем с центром окружности A. Полученный ∠NAB равен третьей части ∠MAB.

Из приведенного описания построения кривой AC трисекции угла видим, что она не сложнее построения квадратрисы Гиппия, а способ пользования кривой AC проще и нагляднее.