2. Вывод уравнения конхоиды

Рассмотрим конхоиду прямой AB с полюсом в точке O (рис. 23). Пусть a - расстояние полюса O до прямой AB, а b - параметр. Пусть M - произвольная (текущая) точка конхоиды, координаты которой относительно некоторой системы координат XOY суть x и y. Найдем уравнение, которому удовлетворяют x и y. Для этой цели выберем систему координат XOY так, чтобы начало координат находилось в полюсе O, ось OX пошла по прямой OK, а ось OY - параллельно AB.

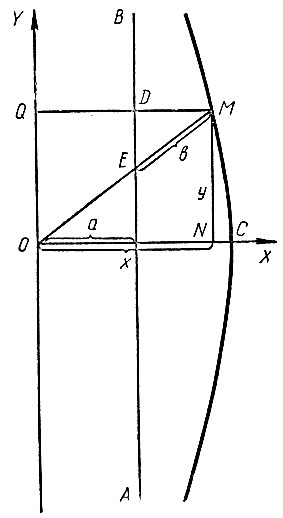
Рис. 23

Опустим из точки M на оси OX и OY соответственно перпендикуляры MN и MQ. Обозначим через D точку пересечения прямых AB и MQ, а через E - точку пересечения прямых AB и OM. Из чертежа легко усмотреть, что 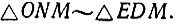Откуда

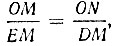
или

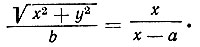
Возводя в квадрат обе части полученного уравнения и освобождаясь от дробности, получим:

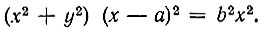
Это и будет искомое уравнение конхоиды.

Выходит, что конхоида Никомеда есть алгебраическая кривая четвертого порядка.