
Глава IV. Вывод уравнений квадратрисы и конхоиды
1. Вывод уравнения квадратрисы
Пусть прямая BC движется равномерно со скоростью v сверху вниз, оставаясь параллельной OA, а прямая OB вращается равномерно с угловой скоростью со по ходу часовой стрелки вокруг точки O (рис. 22). Далее, пусть за время T прямая BC перейдет из положения BC в положение OA и за это же время T прямая OB повернется на прямой угол из положения OB в положение OA. Положим, что за время t прямая BC будет в положении QR, а прямая OB в положении OM. В этом случае точка M будет лежать на квадратрисе BMD, соответствующей квадрату OACB. Примем направления OA и OB за оси координат и обозначим соответственно через OX и OY. Пусть x и y будут координатами точки M.
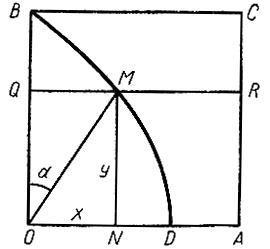
Рис. 22
Найдем теперь уравнение, которому удовлетворяют x и y одновременно. Прежде всего заметим:
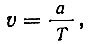
где a - сторона данного квадрата. Исходя из чертежа, замечаем, что
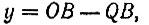
или
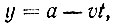
откуда

Обозначим угол BOM через a, получим
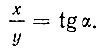
Имея в виду, что 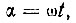 будем иметь:
будем иметь:
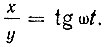
Принимая во внимание, что 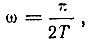 получим:
получим:

Определим t из соотношения (1)
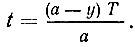
Подставив полученное значение t в соотношение (2),
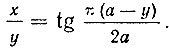
Последнее уравнение можно представить так:
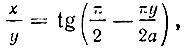
откуда
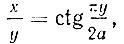
или
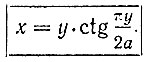
Это и будет искомое уравнение квадратрисы.
Заметим, что для решения задачи о квадратуре круга с помощью квадратрисы надо знать координаты точки D, т. е. координаты нижнего конца квадратрисы. Ордината этой точки равна нулю, а абсцисса находится при помощи формулы:
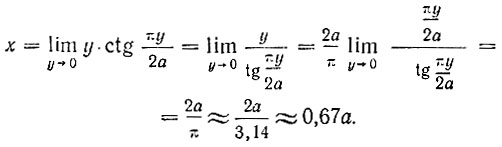
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'