6. Приближенная квадратура круга у народов Средней Азии и ближнего Востока

Среднеазиатские народы имеют за своими плечами богатую самобытную культуру, корни которой уходят в глубину веков. Особенно большой вклад внесли среднеазиатские ученые в мировую математическую культуру, являясь зачинателями ряда научных математических дисциплин и особенно астрономии, алгебры, тригонометрии.

Исторические исследования последних лет показывают, что первое место в развитии математики в странах арабского халифата на протяжении более 500 лет, с IX по XVI в., неизменно принадлежало ученым народов Средней Азии и Закавказья и прежде всего таджикам, узбекам и азербайджанцам. Совершенно прав А. П. Юшкевич, подчеркивая, что "Достижения среднеазиатских математиков IX-XV вв. принадлежат, таким образом, в подавляющей своей части народам нашей страны и поэтому должны привлечь особое внимание советских историков науки" (А. П. Юшкевич, О математике народов Средней Азии в IX-XV вв., "Историко-математические исследования", вып. 4, ГИТТЛ, 1951, стр. 45).

Из ранних среднеазиатских ученых много занимался приближенной квадратурой круга известный хорезмийский алгебраист первой трети IX в. ал-Хорезми (Мухамед бен Муса ал-Хорезми), прославивший себя двумя трактатами: один по алгебре "Хисаб ал-джебр вал-мукабала", а другой по арифметике "Арифметика" ал-Хорезми.

Ал-Хорезми жил при дворе халифа ал-Мамуна, покровителя и ценителя наук, по велению которого переводились древнегреческие классики ("Начала" Евклида, "Конические сечения" Аполлония и работы Архимеда "Об измерении круга", "О шаре и цилиндре", "Алмагест" Птоломея и многие другие), а также извлечения из работ индийских ученых Ариабхата и Брамагупты. Ал-Хорезми успешно занимался вопросами астрономии (уточнил таблицы хорд Птолемея) и принимал участие при измерении градуса земного меридиана. Ал-Хорезми оставил еще ряд трактатов, в том числе "Трактат по астролябии" и "Трактат о солнечных часах".

Своими сочинениями ал-Хорезми много содействовал распространению индийской системы счисления, без которой вряд ли можно было бы в Европе получить "лудольфово число", а также другие, более точные европейские приближения числа π.

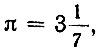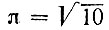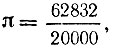Ал-Хорезми познакомил свои и европейские народы с наиболее важными греческими и индийскими приближениями числа &3960;. Он знакомил читателя с архимедовым числом и подчеркивал, что это число является "наиболее употребительным в практике". Об индийских приближениях числа π, которыми являются и он говорит как о наиболее точных результатах и подчеркивает их индийское происхождение.

В так называемой "арабской" литературе имеется сочинение "О квадратуре круга" математика ал-Хайтама (умер в 1038 г.), которое целиком посвящено квадратуре круга, но, к сожалению, оно еще до сих пор широко не обнародовано. Один из знатоков истории квадратуры круга профессор Ф. Рудио высказывает сожаление по поводу того, что это сочинение "еще никем не исследовано, между тем как это первое, известное нам со времен Архимеда, сочинение с таким заглавием и, судя по имени автора, следует ожидать найти в нем интересные попытки подойти возможно ближе к площади круга" (Ф. Рудио, О квадратуре круга с изложением истории вопроса. Перевод с немецкого, под редакцией и с примечаниями акад. С. Н. Бернштейна, изд. 3-е, ОНТИ НКТП СССР, М.-Л., 1936, стр. 39).

В XV в. приближенной квадратурой круга успешно "занимался иранский математик ал-Каши (Джемшид Гиясэддин ал-Каши), посвятивший этому вопросу "Трактат об окружности".

Отдавая дань религиозным суевериям, ал-Каши начищает свой трактат так: "Хвала Аллаху, обладающему знанием отношения диаметра к окружности, знающему величину всего сложного и простого, творцу земли и небес, создателю света во тьме". Говоря о цели своего сочинения, Цв предисловии к нему он писал: "...мы хотим так определить окружность круга в частях, в которых выражен диаметр, чтобы мы были уверены, что в круге, диаметр которого равен шестистам тысячам диаметров земли, разница между рей (полученной величиной окружности) и истинной была не больше волоса, т. е. одной шестой ширины среднего (ячменного зерна, так что разность для круга меньше чем этот не измерялась бы ничем (из этих мер) (Джемшид Гиясэддин ал-Каши, Ключ арифметики и трактат об окружности, Перевод с арабского Б. А. Розенфельда, редакция Б. А. Сегала и А. П. Юшкевича, ГИТТЛ, М., 1956, Игр. 266).

В "Трактате об окружности" ал-Каши дает приближенное вычисление числа 2я с 17 десятичными знаками, выражая это число дробью со знаменателем 10¹⁶. Полученный ал-Каши результат можно записать так:

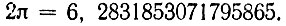
Этот результат верен во всех разрядах.