5. Приближенная квадратура круга у древних индийцев

Самым старым памятником индийской геометрии, дошедшим до нашего времени, являются сборники, имеющие общее название "Сулва-сутры", в буквальном переводе "Правило веревки", составление которых охватывает период с VI до IV в. до н. э. "Сулва-сутра" составляют свод инструкций для построения жертвенников с математическим расчетом их формы, размеров и ориентацией западно-восточной линии.

Для квадратуры круга в "Сулва-сутрах" дается такое индийское правило: "Надо разделить диаметр круга на 15 равных частей и взять 13 таких частей для стороны квадрата, равного кругу".

Легко подсчитать, что в этом случае число 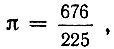или

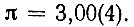
Занимаясь астрономией, индийцы большое внимание уделяли приближенной квадратуре круга и спрямлению окружности и ее частей. В связи с этим им приходилось находить различные приближения для числа π. Так, в VI в. один из виднейших индийских математиков Ариабхата в своем астрономо-математическом сочинении "Ариабхатиам" для приближенного значения я давал значение 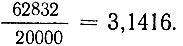Само правило гласило: "Прибавь 4 к 100, умножь на 8, приложи 62 000, это будет приблизительно длина окружности для диаметра, равного 20 000".

В VII в. крупнейший индийский математик Брамагупта предлагал два приближенных значения для я. Одно приближение грубое и равняется 3, т. е. π = 3. Другое приближение более точное и равняется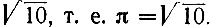

В первой половине XII в. виднейший индийский математик Бхаскара-Акария в своем астрономо-математическом сочинении "Сидданта-сиромани" (венец системы) посвящает математике главу "Лилавати" (прекрасная), где для числа π дает новое приближение, равное дроби 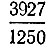, т. е.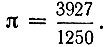

Свое приближение 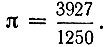он даже называл "точным" в противоположность архимедову значению 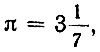которое он считал "неточным".

Весьма точное приближение 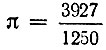Бхаскара находил при помощи формулы:

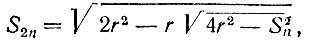
где 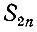- сторона правильного вписанного в круг 2n-угольника, 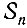- сторона вписанного в круг правильного n-угольника и r - радиус круга.

Заметим, что к квадратуре круга имеют прямое отношение такие два правила Бхаскары.

Первое правило Бхаскары (для определения хорд).

Пусть будет c - окружность, a - дуга, D - диаметр и G - хорда, тогда будем иметь:

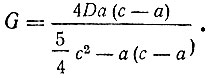
Так, если диаметр равен 240, то хорды дуг в 20, 40, 60, 80, 100, 120, 140, 160 и 180 градусов соответственно будут равны 42, 82, 120, 154, 184, 208, 226, 236 и 240.

Второе правило Бхаскары (для определения дуг).

Формула, определяющая дугу a в функции хорды G для окружности c и диаметра D, будет иметь вид:

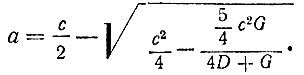
Эту формулу Бхаскара получил из предыдущей, решая уравнение второй степени относительно a.