4. Приближенная квадратура круга у древних китайцев

Одним из замечательных памятников древнего Китая является трактат "Математика в девяти книгах", составление которого относится к началу нашей эры. Первая книга этого трактата посвящается "Измерению полей" и содержит набор задач на вычисление площадей полей различной геометрической формы (прямоугольных, треугольных, в виде трапеций, круга, сегмента, сектора и кольца). Площади круга, сектора и кольца вычисляются при π = 3.

Для вычисления площадей "круглых полей" древние китайцы имели следующие правила.

Первое правило. "Умножь половину обвода на половину диаметра". Таким образом, имеем:

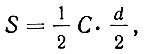
где C - обвод (длина окружности), d - ее диаметр. 60

Второе правило. "Умножь обвод на диаметр, раздели на 4 и возьми один раз". Следовательно, получим:

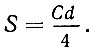
Третье правило. "Умножь диаметр сам на себя, раздели на 4 и возьми 3 раза". Откуда

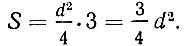
Во II в. китайский математик Чжан Хэн полагает, что 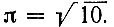Этим приближением пользовался крупнейший индийский математик Брамагупта.

В III в. крупный китайский математик Лю Хуэй путем рассмотрения вписанного в круг правильного многоугольника с 192 сторонами получил для π значение 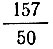т. е. л = 3,14.

В V в. выдающийся китайский математик Цзу Чунжи (430-501) для π получил приближение 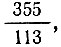дающее семь верных значений цифр, и показал, что число π лежит в пределах:

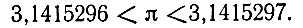
Прошло более 10 веков, когда в XVI в. это приближение было вновь переоткрыто в Нидерландах математиком Андрианом Мецием. Число 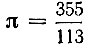в Европе называют "числом Меция".

До XIV в. точность вычисления числа π, данная Цзу Чунжи, была самой высокой во всей мировой науке. Эту точность числа π впервые удалось перекрыть среднеазиатскому математику Джемшиду Гиясэддину ал-Каши, который для я нашел значение с 16 верными десятичными знаками.