3. Приближенная квадратура круга у древних греков

Выше говорилось, что древние греки очень рано стали заниматься квадратурой круга. Еще в V в. ею, как известно, занимался Анаксагор из Клазомен. По свидетельству Платона, Анаксагор дал приближенную квадратуру круга, но это решение до нас не дошло.

По существу приближенную квадратуру круга дал Антифон, который квадрировал круг, как указывалось выше, последовательностью вписанных в круг правильных многоугольников, стороны которых все время удваиваются.

Позднее Бризон для приближенной квадратуры круга стал рассматривать, кроме вписанных в круг правильных многоугольников, стороны которых все время удваиваются, еще и описанные около круга правильные многоугольники, стороны которых также удваиваются.

Если Антифон указал путь, двигаясь по которому можно найти для я нижнюю границу, то Бризон показал, как найти и верхнюю границу π, и в этом смысле пошел дальше Антифона.

Большой вклад в теорию и практику приближенной квадратуры круга в III в. до н. э. внес Архимед из Сиракуз. Он посвятил вопросам приближенной квадратуры круга свой знаменитый трактат "Измерение круга", роль которого в науке трудно переоценить.

В этом трактате Архимед доказывает следующие три теоремы.

Теорема первая. Площадь круга равна площади прямолинейного треугольника, один из катетов которого равняется длине окружности круга, а другой - радиусу круга.

Теорема вторая. Площадь круга относится к площади квадрата, построенного на диаметре, приблизительно, как 11:14.

Теорема третья. Длина окружности превышает утроенный диаметр менее чем на одну седьмую, но больше чем на десять семьдесят первых диаметра.

На языке символов последняя теорема запишется так:

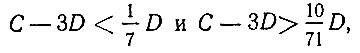
где C - длина окружности, а D - ее диаметр. Откуда

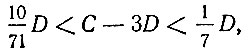
или

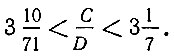
Следовательно,

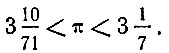
Верхнюю 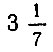и нижнюю 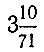границы для числа π Архимед получил путем последовательного рассмотрения отношений периметров к диаметру правильных описанных и вписанных в круг многоугольников, начиная с шестиугольника и кончая 96-угольником. Если я приравнять верхней границе, то получим архимедово значение 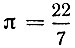(архимедово число), которое, будучи выражено десятичной дробью, дает часто употребляемое приближение с точностью до 0,01.

С приближенной квадратурой круга тесно связано также и имя знаменитого основоположника геоцентрической системы мира древнегреческого ученого Клавдия Птолемея (Ив.), написавшего "Великое математическое построение астрономии в XIII книгах", известное под арабизированным названием "Альмагест". Свое сочинение Птолемей как раз начинает с рассмотрения приближенной квадратуры круга, которая понадобилась ему для составления таблиц синусов.

Птолемей, пользуясь шестидесятеричной системой счисления, значение π выражает числом 3,8'30", т. е.

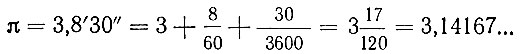
Птолемеево значение числа я, как легко видеть, является более точным, чем значение я, найденное Архимедом.