§ 5. О приближенной квадратуре круга

Из формулы 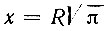видно, чтобы решить задачу о квадратуре круга, достаточно построить отрезок, равный числу π. Но построить отрезок, равный числу π, при помощи циркуля и линейки невозможно, так как число π, как показал Линдеман, есть число трансцендентное. Таким образом, старания древних ученых найти при помощи циркуля и линейки отрезок, длина которого точно равнялась бы числу π, не могли увенчаться успехом и, как следовало ожидать, приводили к приближенным результатам. Само собой разумеется, что если число π вычислять приближенно, то и квадратура круга будет выполняться приближенно. На этот путь приближенного вычисления числа π, начиная с глубокой древности, и встали ученые многих народов.

Рассмотрим историю этого вопроса более подробно.