§ 4. Решение задачи о квадратуре круга при помощи вспомогательных средств

1. Решение Динострата при помощи квадратрисы

Известно, что задача о квадратуре круга неразрешима при помощи циркуля и линейки. Однако задача о квадратуре круга становится вполне разрешимой, если специально для нее расширить средства построения. Это знали еще древние греки. Они знали, что квадратура круга будет вполне разрешимой, если в процессе построения воспользоваться некоторыми специальными кривыми. Первое такое решение задачи о квадратуре круга еще в IV в. до н. э. выполнил Динострат. Он при своем решении воспользовался хорошо известной нам квадратрисой. Суть этого решения заключается в следующем.

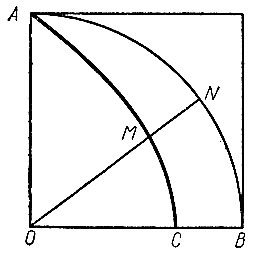
Рис. 21

Пусть ANB - четверть окружности, расположенной в квадранте AOB, а AMC - квадратриса этого квадранта (рис. 21). Далее Динострат воспользовался соотношением, которое позднее было доказано Паппом Александрийским:

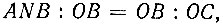
где C - конечная точка квадратрисы.

Поскольку 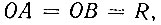то

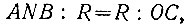
или

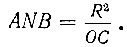
Откуда длина окружности радиуса R равняется 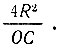Таким образом, длина окружности определена. Чтобы построить квадрат, равновеликий кругу, Динострат, по-видимому, воспользовался теоремой: площадь круга равна площади треугольника, основание которого равно окружности, а высота - радиусу круга^*.

^* (Эта теорема позднее была строго доказана Архимедом и поэтому носит название "теоремы Архимеда".)