§ 3. О доказательстве невозможности решить задачу о квадратуре круга при помощи циркуля и линейки

Попытки древнегреческих ученых решить задачу о квадратуре круга путем проведения прямых и окружностей так и не увенчались успехом. Оно и понятно, почему. Дело в том, что задача о квадратуре круга, так же как и задачи об удвоении куба и трисекции угла, оказывается также неразрешимой при помощи циркуля и линейки.

Еще в 1755 г. Парижская Академия наук, видя бесплодные усилия математиков, а еще больше нематематиков, пытавшихся во что бы то ни стало решить задачу о квадратуре круга, вынесла решение впредь не принимать на рассмотрение работы, касающиеся квадратуры круга, а также и других двух знаменитых задач древности, т. е. задач о трисекции угла и удвоении куба. Это охладило пыл "квадратурщиков", и задачей о квадратуре круга люди стали заниматься значительно меньше.

Окончательный удар всем иллюзиям решить задачу о квадратуре круга при помощи циркуля и линейки был нанесен лишь во второй половине XIX в. Немецкому математику Ф. Линдеману в 1882 г. удалось, наконец, вполне строго доказать, что задача о квадратуре круга неразрешима при помощи циркуля и линейки и все старания что-нибудь сделать в этом направлении указанными средствами являются совершенно напрасными и ненужными.

Доказательство Линдемана чрезвычайно трудное и далеко выходит за пределы школьного курса математики.

Оставляя в стороне рассуждения Линдемана о невозможности решения квадратуры круга, мы ограничимся следующими весьма краткими замечаниями.

Пусть дан круг радиуса R и требуется построить квадрат, равновеликий этому кругу. Обозначим сторону искомого квадрата через x, тогда будем иметь:

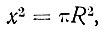
откуда

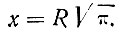
Таким образом, вопрос о построении квадрата, равновеликого данному кругу, сводится к построению произведения данного отрезка R на данное число 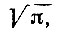причем это построение надо провести при помощи только циркуля и линейки, т. е. путем проведения конечного числа окружностей и прямых линий.

При помощи циркуля и линейки можно всегда построить произведение данного отрезка R на рациональное число (целое или дробное), но далеко не всегда можно указанными средствами построить произведение данного отрезка на число иррациональное. Произведение данного отрезка R на число иррациональное можно построить в некоторых случаях, если, например, иррациональное число равняется 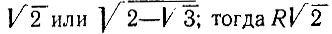находится, как сторона квадрата, вписанного в круг радиуса R, а 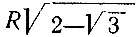- как сторона правильного 12-угольника, вписанного в круг радиуса R, причем, как известно, вписать правильный 12-угольник в круг не составляет трудности, после того как в круг предварительно вписан правильный шестиугольник.

В теории геометрических построений установлено, что данный отрезок R можно умножить при помощи циркуля и линейки на вещественное число лишь только в том случае, если это вещественное число может быть корнем алгебраического уравнения с целыми коэффициентами, разрешимого в квадратных радикалах. Число, которое не может являться корнем никакого алгебраического уравнения с целыми коэффициентами, принято называть трансцендентным числом. Следовательно, при помощи циркуля и линейки нельзя построить произведение данного отрезка R на число трансцендентное. Таким образом, чтобы доказать неразрешимость задачи о квадратуре круга при помощи циркуля и линейки, необходимо установить невозможность указанными средствами построить произведение данного отрезка R на число 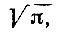а для этого достаточно показать, что 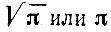есть число трансцендентное.

Заслуга Ф. Линдемана как раз и заключается в том, что он впервые в мировой науке вполне строго доказал, что я есть число трансцендентное и тем самым окончательно установил невозможность решения задачи о квадратуре круга с помощью циркуля и линейки. Вот почему Ф. Линдемана называют "победителем числа π", а еще лучше - "победителем задачи о квадратуре круга"^*.

^* (См. по этому поводу статью И. Я. Депмана "Победитель числа π - Фердинанд Линдеман". "Ученые записки" Ленинградского госуд. пединститута. Физико-математический факультет, т. XVII, вып. 2, стр. 119-123.)

В заключение заметим, что изучение арифметической природы числа я исторически шло в следующем направлении. Сначала в 1761 г. немецкий математик И. Ламберт первый показал, что число я есть число иррациональное. Позднее французский математик А. Лежандр установил, что квадрат числа я есть также число иррациональное. Наконец, в 1882 г. немецкий математик Ф. Линдеман доказал знаменитую теорему, согласно которой, как указывалось выше, число я есть число трансцендентное, т. е. оно не может служить корнем какого-нибудь алгебраического уравнения с целыми коэффициентами. Отсюда, как следствие, уже вытекала неразрешимость с помощью циркуля и линейки знаменитой задачи о квадратуре круга.