§ 2. Попытка решить задачу о квадратуре круга при помощи циркуля и линейки

Древнегреческие ученые стремились задачу о квадратуре круга решить при помощи циркуля и линейки. Показательна в этом отношении работа Гиппократа Хиосского, которому удалось криволинейную фигуру (гиппократовы луночки) преобразовать в равновеликий ей многоугольник. Однако преобразовать круг в равновеликий ему квадрат Гиппократу так и не удалось. Остановимся несколько подробнее на его рассуждениях.

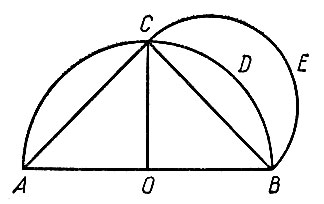
Рис. 19

На отрезке AB, как на диаметре (рис. 19), построим полукруг ABC. Далее, из точки O - середины отрезка AB - восставим перпендикуляр OC. Соединим прямыми точку C с точками A и B. Отрезок CB будет стороной квадрата, вписанного в круг, и площадь треугольника ACB будет равняться половине этого квадрата. На отрезке CB, как на диаметре, опишем еще полукруг CEB. Применяя к прямоугольному треугольнику ACB теорему Пифагора, получим:

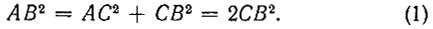
На основании того, что площади кругов относятся между собой, как квадраты их диаметров, будем иметь:

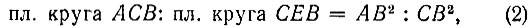
или, учитывая (1),

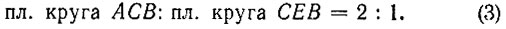
Откуда

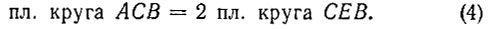
Тогда

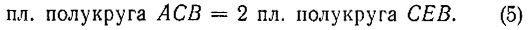
Следовательно,

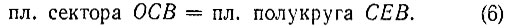
Вычитая из левой и правой частей равенства (6) сегмент CDB, получим, что площадь 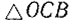равняется площади луночки CDBE. Наконец, при помощи циркуля и линейки теперь не составляет большого труда построить квадрат, площадь которого будет равна площади 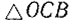, а следовательно, и площади луночки CDBE. Так Гиппократ Хиосский весьма оригинальным приемом нашел квадратуру некоторой, специального вида, луночки.

Это открытие Гиппократа окрылило древних геометров надеждой, что с помощью циркуля и линейки когда-нибудь удастся вычислить и квадратуру круга: "Раз можно найти квадратуру некоторой луночки, образованной дугами кругов, то почему же,- рассуждали они, - нельзя найти квадратуру круга".

Сам Гиппократ, найдя квадратуру указанной выше луночки, пытался найти квадратуру круга, пользуясь следующими рассуждениями. Пусть дан произвольный круг Диаметра AB и требуется, пользуясь только циркулем и линейкой, построить квадрат, равновеликий этому кругу.

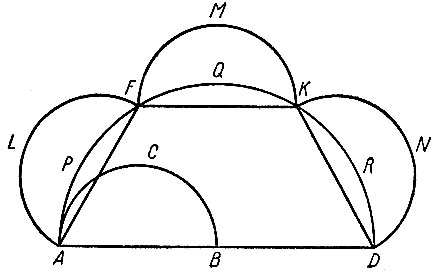
Рис. 20

Рассмотрим полукруг ACB данного диаметра AB (рис. 20). Возьмем отрезок AD, равный удвоенному диаметру AB, и построим на нем, как на диаметре, полуокружность. Далее, раствором циркуля, равным AB, находим на полуокружности точки F и K. Концы дуг AF, FK и KD соединяем хордами, которые образуют трапецию AFKD, вписанную в полуокружность AFKD. Боковые стороны AF и KD и верхнее основание FK этой трапеции равны между собой и равны AB - по построению. Построим на отрезках AF, FK и KD, как на диаметрах, полуокружности ALF, FMK, KND.

Известно, что площади кругов относятся, как квадраты их диаметров. Следовательно,

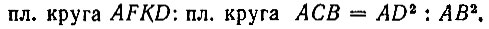
Но AD = 2AB, тогда

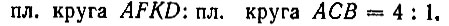
Откуда

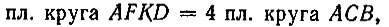
или

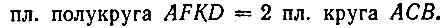
Окончательно имеем;

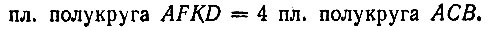
Так как 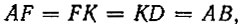то площади полукругов ALF, FMK и KND, взятые по отдельности, равны площади полукруга ACB. Учитывая это, будем иметь:

Вычитая из левой и правой частей площади сегментов APF, FQK и KRD, которые являются общими частями большого полукруга AFKD и соответственно малых полукругов ALF, FMK и KND, получим:

Откуда

Выходит, что площадь данного круга ACB равна удвоенной разности площади трапеции и некоторого квадранта. Следовательно, для данного круга, как думал Гиппократ, можно указанным способом всегда построить квадрат, равновеликий этому кругу, пользуясь только циркулем и линейкой.

Однако в рассуждениях Гиппократа Хиосского допущена одна ошибка, которая "из невозможного делает возможным" - неразрешимую задачу о квадратуре круга разрешимой. Ошибка в рассуждениях Гиппократа, приводящая к иллюзорному решению задачи о квадратуре круга, была замечена еще древними учеными. Об этой ошибке говорят древнегреческий историк математики Евдем Родосский и знаменитый основоположник формальной логики Аристотель. Так, Евдем Родосский заявляет, что хотя рассуждение Гиппократа Хиосского и является остроумным, тем не менее оно является ошибочным. Дело в том, говорит Евдем, что три луночки, которые рассматривал Гиппократ при решении квадратуры круга, построены не на катетах прямоугольного треугольника, а на сторонах трапеции и, следовательно, к ним он не может применить то свойство о квадрируемости луночки, которое он доказал в начале. В этом же упрекал Гиппократа и Аристотель. Аристотель, как и Евдем, считал, что Гиппократ впал в грубую ошибку, полагая возможным квадратуру луночки, построенной на стороне квадрата, необдуманно применить к квадратуре луночки, построенной на стороне шестиугольника^*.

^* (Некоторые ученые истории математики (Лакруа, Бретшнейдер) говорят, что, несмотря на свидетельство древних историков, они не верят, чтобы такой проницательный геометр, как Гиппократ, впал в такую грубую ошибку. Вероятно, заявляют они, сам Гиппократ выразился следующим образом: если бы квадратура луночки, построенной на стороне шестиугольника, была возможной, то и квадратура круга также была бы возможной. Но его комментаторы исказили смысл приведенной фразы и дали повод обвинять Гиппократа в том, в чем сам он, по-видимому, совершенно не виноват.)

Другая попытка решить задачу о квадратуре круга с помощью циркуля и линейки была предпринята древнегреческим ученым Антифоном. Он в данный круг, квадратура которого находилась, вписывал сначала квадрат. Затем дуги, хордами которых являются стороны вписанного в круг квадрата, он делил пополам и точки деления соединял с вершинами квадрата и таким образом получал вписанный в круг правильный восьмиугольник. Далее, дуги, хордами которых являются стороны вписанного в круг правильного восьмиугольника, делил также пополам и точки деления соединял с вершинами указанного восьмиугольника и получал вписанный в круг правильный 16-угольник. Продолжая этот процесс дальше, он получал вписанные в круг правильные 32-угольник, 64-угольник и т. д. Он считал, что указанным построением, выполняемым только при помощи циркуля и линейки, можно прийти к такому правильному многоугольнику, правда, быть может, с очень большим числом сторон, который полностью исчерпает круг, т. е. его площадь будет равна площади данного круга. А так как для любого правильного многоугольника всегда можно построить равновеликий ему квадрат, то и для данного круга, поскольку он исчерпывается правильным многоугольником, можно построить равновеликий ему квадрат.

Еще в древности ученые подвергли решение Антифона резкой критике. Они совершенно правильно заявляли, что утверждение Антифона, будто правильный многоугольник может совпасть с кругом, противоречит основным началам геометрии.

Однако для целей приближенной квадратуры круга рассуждение Антифона вполне приемлемо, так как с помощью этого рассуждения данный круг можно приближенно квадрировать с любой степенью точности.