3. Решение Архимеда при помощи циркуля и линейки с двумя отметками

Оригинальное и вместе с тем чрезвычайно простое решение задачи о трисекции угла дал древнегреческий ученый Архимед.

О жизни Архимеда известны только отрывочные сведения, которые дошли до нас благодаря древним писателям Цицерону, Плутарху и другим. Из их работ узнаем, что Архимед родился в 287 году до н. э. в Сицилии и на 75 году жизни был убит римским воином при взятии римлянами города Сиракуз в 212 году до н. э.

Рассказывают, что Архимед был патриотом своей родины и города Сиракуз, где он родился и жил. Он в течение двух лет при помощи своих машин с успехом защищал Сиракузы от мощной римской армии, которой командовал Марк Клавдий Марцелл, один из самых крупных военачальников того времени. Вот в каких словах передает древнегреческий писатель Плутарх (ок. 46-126) взятие города Сиракуз римлянами;

"Марцелл вполне полагался на обилие и улеск своего вооружения и на собственную свою славу. Но все оказалось беспомощным против Архимеда и его машин...

Архимед

Архимед был родственником умершего царя Гиерона. В свое время Архимед писал Гиерону, что небольшой силой возможно привести в движение сколь угодно большую тяжесть; более того, вполне полагаясь на убедительность своих доказательств он утверждал даже, что был бы в состоянии привести в движение самую Землю, если бы существовала другая, на которую он мог бы стать ("Дайте мне, где стать, и я сдвину Землю"). Гиерон был этим удивлен и предложил Архимеду показать на деле, как возможно большую тяжесть привести в движение малой силой. Архимед осуществил это над грузовым трехмачтовым судном, которое, казалось, могло вытащить на берег только большое число людей. Архимед велел посадить на судно множество людей и нагрузить его большим грузом. Поместившись затем в некотором отдалении на берегу, он без всякого напряжения, очень спокойно нажимая собственной рукой на конец полиспаста, легко, не нарушая равновесия, придвинул судно. Гиерон был этим в высшей степени поражен и, убедившись в высоком значении этого искусства, склонил Архимеда соорудить машины как для обороны, так и для нападения при любой осаде...

Архимед посредством машины вытаскивает на берег галеру

Когда римляне начали наступление с суши и с моря, сиракузяне считали невозможным противостоять такой большой силе и военной мощи. Но когда Архимед привел в действие свои машины и орудия разнообразного рода, на сухопутные войска врагов посыпались камни огромной величины и веса с шумом и невероятной быстротой. Целые подразделения войск валились на землю, и их ряды пришли в полный беспорядок. В то же время и на суда неприятеля обрушивались из крепости тяжелые балки, искривленные в виде рогов; одни из них сильными ударами погружали суда в глубь моря, другие крюками в форме журавлиных клювов, точно железными руками, поднимали корабли высоко в воздух, а затем опускали кормой в воду. В то же время другие машины швыряли суда на скалы возле стен города, и их матросы подвергались страшному уничтожению...

Римляне были так напуганы, что достаточно было показаться над стенами канату или деревянной палке, как все кричали, что Архимед направил на них машину, и быстро убегали. Видя это, Марцелл прекратил сражение и нападение и предоставил дальнейшую осаду действию времени".

В своих математических расчетах Архимед, предвосхитив идеи современного математического анализа, остроумно решал задачи на вычисление длин кривых, площадей и объемов.

Смерть Архимеда

До нас дошли следующие сочинения Архимеда:

1. Две книги о шаре и цилиндре,
2. Измерение круга.
3. О коноидах и сфероидах.
4. О спиралях.
5. Две книги о равновесии плоскости.
6. Исчисление песчинок.
7. Квадратура параболы.
8. Послание Эратосфену о методе обработки механических предложений.
9. Две книги о плавающих телах.
10. Отрывки.

Задачу о трисекции угла Архимед решает при помощи обыкновенного циркуля и подвижной линейки, на которой разрешается делать две отметки, расстояние между которыми должно равняться радиусу проводимой окружности. Как это делается, покажем на конкретном примере. Пусть требуется произвольно взятый острый угол ABC разделить на три равные части. Для этого из вершины данного угла B, как из центра, произвольным радиусом R опишем окружность (рис. 18). Точки пересечения сторон данного угла с окружностью обозначим через D и E. Теперь берем подвижную линейку с двумя отметками F и G, причем длина отрезка FG - R, и прикладываем ее к точке E так, чтобы F и G оказались на одной прямой с точкой E и чтобы F находилась на окружности, а G - на продолжении стороны В А. Тогда угол EGD и будет составлять одну треть заданного угла ABC.

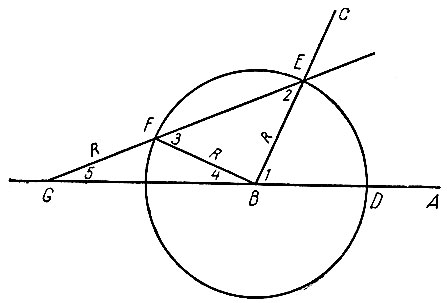
Рис. 18

Докажем это. Обозначим для краткости углы на чертеже цифрами 1, 2, 3, 4, 5. Надо доказать, что угол 5 составляет третью часть угла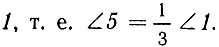

Действительно, 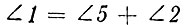(свойства внешнего угла треугольника), но 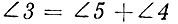(свойство внешнего угла треугольника). Далее, 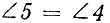(свойство равнобедренного треугольника). Тогда 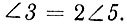Из треугольника BEF, поскольку он равнобедренный, 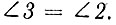Учитывая предыдущее равенство, будем иметь:

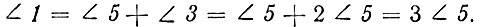
Следовательно,

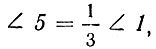
что и требовалось доказать.