2. Решение Паппа Александрийского при помощи конхоиды Никомеда

Во II в. до н. э. в Александрии жил ученый Никомед. Жизнь его, как и многих других ученых древней Греции, нам почти неизвестна. В своих комментариях к первой книге "Начала" Евклида Прокл утверждает, что Никомед изобрел конхоиду, которую он использовал для решения задачи об удвоении куба и трисекции угла. Однако Папп Александрийский, живший в IV в. н. э., в своих "Математических коллекциях", посвященных жизнеописанию древнегреческих ученых, где он подробно останавливается на знаменитых задачах древности, подтверждает, что Никомед действительно изобрел замечательную кривую, названную им конхоидой, которую с успехом можно применить к решению задачи о трисекции угла, но это было сделано уже после Никомеда. Заслугу применения конхоиды Никомеда к решению задачи о трисекции угла Папп приписывает себе.

А теперь посмотрим, как, следуя Паппу, можно при помощи конхоиды решить задачу о трисекции угла.

Прежде всего поближе познакомимся с самой конхоидой Никомеда. Пусть имеется некоторая прямая AB (базис) и точка O (полюс) вне этой прямой. В плоскости, определяемой ими, через точку O проведем пучок лучей и на каждом луче отложим равные отрезки в обе стороны от его точки пересечения с данной прямой. Геометрическое место концов этих отрезков и представляет конхоиду Никомеда, т. е. конхоиду прямой AB относительно полюса O^*.

^* (Вообще говоря, можно построить конхоиду, приняв за базис кую-нибудь кривую линию, но Никомед такую конхоиду не рассматривал.)

На чертеже (рис. 16) изображены три конхоиды прямой относительно полюса О, отвечающие трем случаям: a>b, a = b и a<b, где a - расстояние полюса O до базиса AB и b - откладываемый отрезок (параметр).

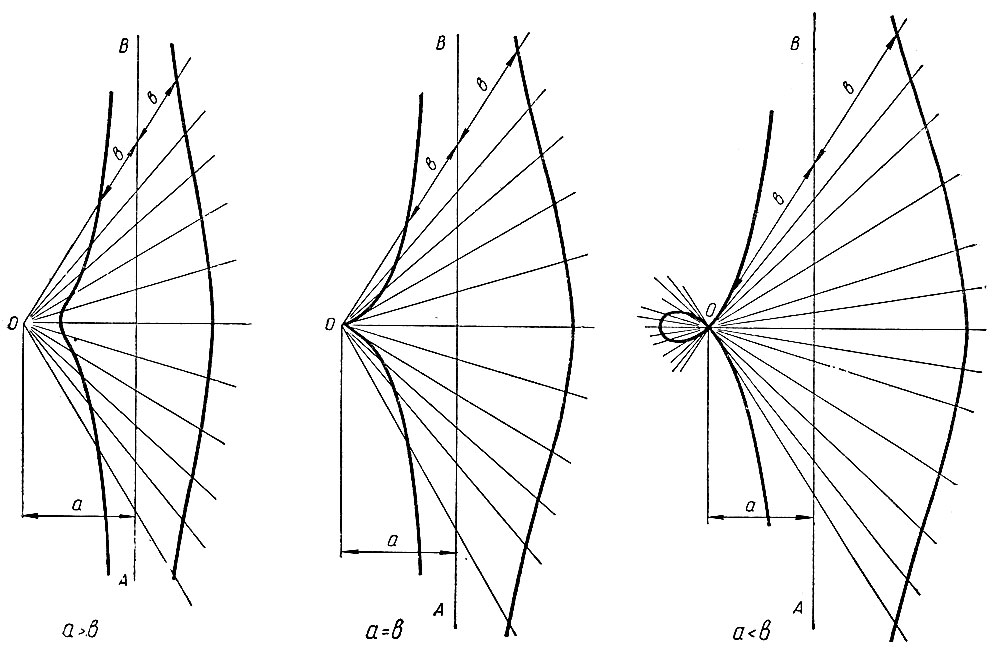
Рис. 16

Пусть теперь требуется "какой-нибудь острый угол AOB разделить на три равные части, причем эту трисекцию надо произвести при помощи конхоиды Никомеда.

Поступаем так, как указывал Папп Александрийский. На одной из сторон данного угла, например на стороне OB, возьмем произвольную точку C и из нее на прямую OA опустим перпендикуляр CD (рис. 17). Теперь построим одну ветвь (правую) конхоиды Никомеда, приняв точку O за полюс, прямую CD за базис, а отрезок, равный 2OC, за параметр. Эта конхоида пересечет стороны данного угла в точках E и F. Через точку С проведем прямую, параллельную DE, которая пересечет конхоиду в некоторой точке K. Соединим точку K с точкой O. Полученный угол AOK и будет составлять одну треть данного. Докажем это. Прежде всего обозначим точку пересечения прямых OK и CD через L. Середину отрезка LK обозначим через M и соединим ее прямой с точкой С. Нужные нам углы, как показано на чертеже, обозначим цифрами 1, 2, 3, 4, 5. Остается доказать, что угол 2 в два раза больше угла 1. Действительно, принимая во внимание свойство конхоиды, будем иметь:

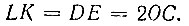
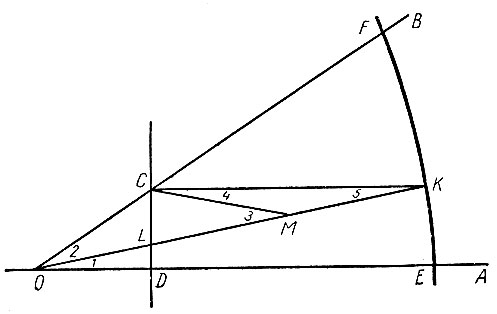
Рис. 17

Далее,

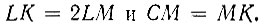
Следовательно,

Далее,

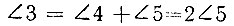
(свойство внешнего угла треугольника),

или

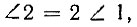
т. е. угол AOK составляет одну треть угла AOB, что и требовалось доказать.