§ 4. Решение задачи о трисекции угла при помощи вспомогательных средств

1. Решение Гиппия из Элиды при помощи открытой им квадратрисы

Задача о трисекции угла в общем случае не разрешима при помощи циркуля и линейки, но это вовсе не значит, что данную задачу нельзя решить другими вспомогательными средствами. Древним геометрам было хорошо известно, что достаточно немного усилить конструктивные возможности циркуля и линейки дополнительными вспомогательными средствами, чтобы трисекция любого угла стала уже выполнимой.

Первый из древнегреческих ученых, кто дал строгое решение задачи о трисекции любого острого угла при помощи дополнительных вспомогательных средств, был Гиппий из Элиды (V в. до н. э.). Для своего решения Гиппий воспользовался открытой им кривой, которую он назвал квадратрисой (от позднелатинского quadratrix). Он даже изобрел механизм, вычерчивающий эту кривую. Квадратрису он получил, исходя из следующих механических соображений. Пусть имеется квадрат ABCD (рис. 13). Предположим, что сторона этого квадрата AD, как подвижный радиус, будет равномерно вращаться вокруг точки A, как своего центра, и за время t опишет четверть окружности от точки D до точки B.

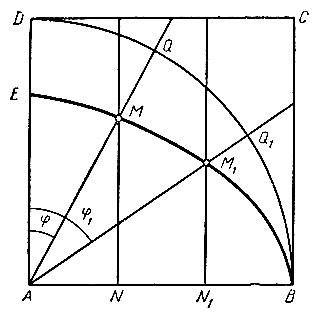
Рис. 13

Пусть далее прямая, перпендикулярная AB, будет равномерно перемещаться слева направо от точки A до точки B и за указанное выше время t перейдет из положения AD в положение BC. Тогда геометрическое место точек пересечения в каждый момент времени вращающегося радиуса и прямой, перемещающейся параллельно самой себе и перпендикулярной AB, образует непрерывную кривую, которая и носит название квадратрисы^*.

^* (Сам термин "квадратриса" стал употребляться с IV в. до н. э. после того, как Динострат - ученик Платона и брат Менехма - применил квадратрису к решению квадратуры круга, о которой речь будет позднее (гл. III).)

Как исследовал Гиппий, квадратриса обладает тем замечательным свойством, что абсциссы ее точек пропорциональны соответствующим углам, т. е.

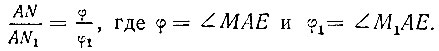
Для доказательства положим, что радиус AD за единицу времени повернется на угол α, а прямая, перпендикулярная AB, за это время переместится на k единиц. Пусть далее, что точки M и M₁ квадратрисы получились соответственно через t и t₁ единиц времени. Тогда

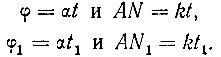
Разделив эти равенства почленно, будем иметь:

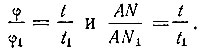
Следовательно,

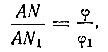
что и требовалось доказать.

Из доказанного, как следствие, вытекает, что равным отрезкам неподвижного радиуса AB при помощи квадратрисы соответствуют и равные дуги окружности DB. Так, на рисунке 13 отрезку AN соответствует дуга DQ, отрезку NN₁ - дуга QQ₁ и отрезку N₁B - дуга Q₁B. Если положить, что AN = NN₁ = N₁B₁, тогда и соответствующие дуги будут равны. Теперь уже без особого труда можно разделить любой острый угол не только на три, но и на любое число равных частей.

Пусть дан острый угол а и требуется разделить его на три равные части.

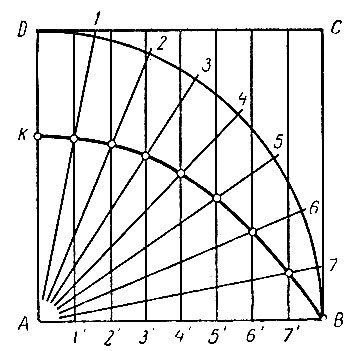
Рис. 14

Сначала построим для некоторого квадрата ABCD квадратрису. Для этого дугу окружности DB и сторону AB данного квадрата разделим на 2n равных частей, где n - любое натуральное число. Заметим, что, чем больше возьмем n, тем точнее будет построение квадратрисы. Для простоты положим n = 4, тогда 2n = 8. Делим дугу DB и радиус AB на 8 равных частей. Концы полученных равных частей дуги DB обозначим цифрами 1, 2, 3, 4, 5, 6, 7 (рис. 14). Точки деления неподвижного радиуса AB обозначим через 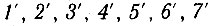Теперь точки 1, 2, 3

4, 5, б, 7 соединим прямыми с точкой A, а через точки 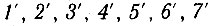проведем прямые, перпендикулярные AB. Точки пересечения полученных радиусов с соответствующими прямыми, перпендикулярными AB, и будут точками квадратрисы (на чертеже обозначены кружочками). Соединяя эти точки плавной кривой, мы и получаем квадратрису KB, как непрерывную линию.

Теперь при помощи квадратрисы разделим данный острый угол а на три равные части. Для этой цели построим угол FAB, равный углу α (рис. 15). Обозначим точки пересечения прямой AF с квадратрисой KB и окружностью DB соответственно через 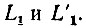Далее из точки L₁ на прямую AB опустим перпендикуляр L₁P. Затем отрезок PB обычным приемом, показанным на чертеже, разделим на три равные части точками Q и R. В точках Q и R к прямой AB восставим перпендикуляры до пересечения их с квадратрисой KB в точках 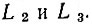Соединяя точки 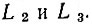с точкой A и продолжая прямые AL₂ и AL₃ до пересечения с окружностью DB, получим точки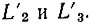

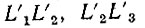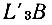Поскольку дуги и равны между собой, то соответствующие им центральные углы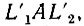 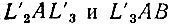также равны между собой и каждый из них равен 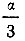Следовательно, указанным выше приемом мы разделили данный угол а на три равные части, что и нужно было сделать.