§ 3. О доказательстве неразрешимости задачи о трисекции произвольного угла при помощи циркуля и линейки

Древнегреческие ученые проявили много тонкого остроумия для изобретения разного рода механизмов, с помощью которых они без особого труда делили произвольный угол на три равные части. Но перед ними всегда стоял вопрос: почему трисекция угла, легко выполнимая при помощи специально изготовленных механизмов, не поддается разрешению при помощи циркуля и линейки? И вообще, разрешима ли эта задача в общем виде при помощи этих классических чертежных инструментов?

Чтобы ответить на поставленный вопрос, проведем некоторые рассуждения. Обозначим данный угол, который требуется разделить на три равные части, через 3α. Рассмотрим cos 3x.

По известным формулам тригонометрии будем иметь:

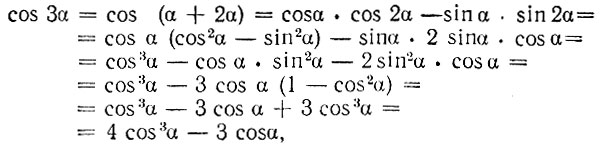
или

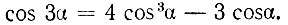
Умножая левую и правую части полученного равенства на 2, будем иметь:

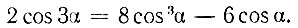
Пусть теперь 2 cos 3α = a и 2 cos α = x, тогда

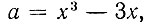
или

Чтобы доказать, что задача о трисекции угла не разрешима в общем виде, достаточно указать хотя бы один угол, который нельзя разделить при помощи циркуля и линейки. Путем несложных рассуждений покажем, что таким свойством обладает, например, угол в 60°. Действительно, полагая 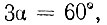получим 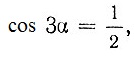и уравнение (1) примет вид:

В алгебре доказывается, что рациональными корнями уравнения (2) могли бы быть +1 и -1, но ни то, ни Другое указанному уравнению не удовлетворяет. Выходит, что уравнение (2) не имеет рациональных корней, и, следовательно, по "теореме неразрешимости" угол в 60° нельзя разделить на три равные части при помощи циркуля и линейки^*. Итак, если пользоваться циркулем и линейкой, задача о трисекции угла в общем виде не разрешима.

^* (Из того, что угол в 60° не может быть разделен на три равные части при помощи циркуля и линейки, вытекает, что угол в 20°, а следовательно, и угол в 40° не могут быть построены указанными инструментами. Отсюда вытекает важное предложение: правильный девятиугольник, восемнадцатиугольник и т. д. не могут быть построены циркулем и линейкой.

Далее, для а можно было бы указать еще бесчисленное множество значений, для которых уравнение (1) не разрешимо в квадратных радикалах, и, следовательно, существует бесчисленное множество углов, трисекция которых не может быть выполнена при помощи Циркуля и линейки.)

Укажем теперь некоторые частные случаи, когда задача о трисекции угла разрешима циркулем и линейкой.

Древним ученым, как указывалось выше, была известна трисекция прямого угла при помощи циркуля и линейки. Возможность этой трисекции можно подтвердить и теоретически. Действительно, положив 3α = 90°, получим, что a = 0, и уравнение (1) примет вид:

Уравнение (3) имеет корни 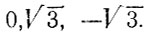Таким образом, ненулевые корни выражены в квадратных радикалах. Следовательно, угол в 90° можно разделить циркулем и линейкой на три равные части.

Аналогичными рассуждениями можно было бы показать, что теми же средствами и угол в 45° можно разделить на три равные части.

Необходимо добавить, что трисекция при помощи циркуля и линейки возможна для бесчисленного множества углов, например для углов вида 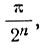где n - целое положительное число (последнее рекомендуется доказать самостоятельно).

Р. Декарт был первым ученым, который высказал предположение, что трисекция произвольного угла не может быть выполнена при помощи циркуля и линейки, если последняя не имеет никаких отметок. Строгое же доказательство неразрешимости задачи о трисекции произвольного угла впервые было дано в 1837 г. П. Ванцелем.