§ 2. Попытка решить задачу о трисекции угла при помощи циркуля и линейки

Пользуясь циркулем и линейкой, древние греки умели делить произвольный угол на две равные части. Со времен Пифагора они умели делить прямой угол на три равные части. Это они выполняли так.

Пусть дан прямой угол ABC и требуется разделить его на три равные части, т. е. произвести трисекцию этого угла. Для этого из вершины данного угла B, как из центра, проводим окружность (для нужного построения достаточно провести четверть окружности). Точки пересечения окружности со сторонами AB и BC соответственно обозначим через M и N (рис. 12). Далее, из точек M и N тем же радиусом делаем засечки R и Q. Теперь соединим хордами M и R, N и Q. Получаем два равносторонних треугольника: ΔBRM и ΔBQN. Но в равностороннем треугольнике все три угла по 60°. Следовательно, ∠ MBR = ∠ QBN = 60°. Тогда ∠ MBQ = ∠ RBN = ∠ QBR = 30°. Итак, данный прямой угол удалось разделить на три равные части. Что и нужно было сделать.

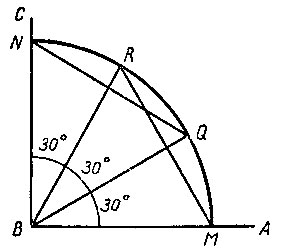
Рис. 12

С такой же легкостью и теми же средствами древние греки стремились разделить на три равные части и всякий другой угол. Но тут их постигло глубокое разочарование. Пользуясь циркулем и линейкой, они смогли выполнить трисекцию углов только для отдельных частных случаев.

В чем дело? А дело заключается в том, что трисекция произвольного угла оказывается неразрешимой при помощи циркуля и линейки, но об этом будет рассказано в следующем параграфе.