8.3. Схевенингекская система и латинские квадраты

(От названия голландского города Схевенинген.)

Множество математических проблем возникает вокруг схевенингенской системы проведения командных встреч. В турнире двух команд каждый участник одной из команд встречается с каждым участником другой. Возникает вопрос о составлении расписания встреч участников. Если в каждой команде по n участников, то весь матч проводится за n туров. Для n = 4 расписание игр приведено на рис. 28. Строки квадрата отвечают игрокам команды I, столбцы - игрокам команды II. На пересечении i-й строки и j-го столбца указан номер тура, в котором играют соответствующие участники. Цвет фигур для участника команды II определяется цветом клетки (штриховкой).

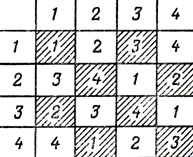
Рис. 28

Для n = 6 может быть предложено расписание, указанное на рис. 29. Каждая строка и каждый столбец квадрата, задающего расписание туров для n = 4, содержит каждую из цифр от 1 до 4 и в точности по одному разу. В квадрате для n = 6 в каждой строке (столбце) встречается любая из цифр от 1 до 6 и притом лишь однажды. Аналогичная ситуация имеет место и для любого n.

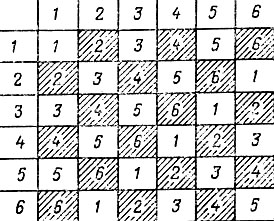
Рис. 29

Квадраты с подобным расположением чисел называют латинскими. До последних лет латинскими квадратами интересовались лишь любители головоломок и некоторые математики. Латинские квадраты стали известны, в основном, благодаря предложенной Леонардом Эйлером (1707 - 1783) в 1782 г. задаче: среди 36 офицеров имеется по шесть офицеров шести различных званий из шести полков. Можно ли построить этих офицеров в каре так, чтобы в каждой колонне и каждой шеренге встречались офицеры всех званий и всех полков?

Лишь в 1901 г. удалось доказать, что такая расстановка невозможна. Однако латинские квадраты (Л. Эйлер в работе с ними использовал не числа, а буквы латинского алфавита) получили в последующем многочисленные приложения, в частности, в комбинаторных задачах, а в конце шестидесятых годов они нашли применение в теории кодирования сообщений (см. [23]).

Мы убедились также, что латинские квадраты имеют непосредственное отношение к организации соревнований. Поэтому продолжим их изучение.

Итак, латинский квадрат - это матрица порядка n, элементами которой являются числа 1, 2, ..., n, каждое из которых ровно один раз содержится в каждой ее строке и столбце.

Две матрицы порядка n называют ортогональными, если при наложении любой из них на другую возникает множество всех упорядоченных пар (i, j), i = 1, ..., n; j = 1, ..., n. Примером ортогональных латинских квадратов (матриц) порядка n = 3 служат

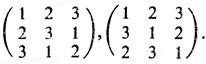
При их наложении возникает новый квадрат

называемый греко-латинским или эйлеровым. Его элементами являются упорядоченные пары чисел (i, j).

Отождествим первую цифру каждой числовой пары с определенным офицерским званием (например, единица - лейтенант, двойка - капитан, тройка - майор и т. п), а вторую цифру пары - с номером полка. Тогда полученный эйлеров квадрат указывает на требуемую расстановку в каре девяти офицеров трех различных званий из трех полков.

Ортогональны также матрицы

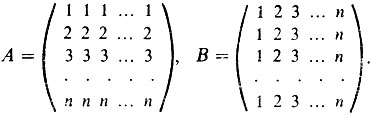
Легко заключить, что матрица порядка n является латинским квадратом тогда и только тогда, когда она ортогональна как матрице A, так и матрице В. В то же время сами эти матрицы латинскими квадратами не являются.

Проблема существования ортогональных латинских квадратов любого порядка оставалась не решенной более 200 лет. В 1779 г. сам Эйлер высказал предположение о том, что ортогональных квадратов порядка n = 4k + 2 (k = 0, 1, 2, ...) не существует. Лишь в 1901 г. Терри доказал справедливость гипотезы Эйлера для п = 6 (т. е. k = 1, для k = 0 она очевидна) путем прямого перебора всех возможностей. Наконец в 1959 г. Паркер нашел эйлеров квадрат порядка n = 10 (т. е. для k = 2) и совместно с Босе и Шарикхандом в 1960 г. доказал существование ортогональных латинских квадратов любого порядка n, за исключением n = 2 и n = 6.

Вернемся вновь к расписанию турнира по схевенингенской системе для n = 6. Видно, что, хотя каждый из участников матча играет одинаковое число партий белыми и черными, обе команды в каждом туре играют все партии одним цветом, что нежелательно (играющая белыми имеет преимущество).

Поэтому поставим задачу построения такого расписания, при котором:

• все участники играют равное число партий белыми и черными;
• в каждом туре каждая команда играет равное число партий белыми и черными.

Естественно, что число n участников с необходимостью должно быть четным. Рассмотрим пару ортогональных латинских квадратов А и В порядка n. Наложим квадрат В на A и заштрихуем все клетки A, на которые пришлись четные числа из квадрата В. Все остальные клетки А оставим белыми.

Так как в каждой строке и в каждом столбце квадрата А половина чисел четна, то сразу видно, что условие а) выполняется. Ввиду ортогональности А и В каждым n одинаковым числам из А соответствует половина четных и половина нечетных чисел из В. Этим удовлетворено также и условие б).

Заметим, что из того, что для п = 6 ортогональных латинских квадратов не существует, еще не следует невозможность построения необходимого расписания. И действительно, путем прямого перебора с помощью ЭВМ удалось

найти серию требуемых расписаний. Одно из них приведено на рис. 30. Оно хорошо тем, что ни один из участников не играет подряд одним цветом более двух партий.

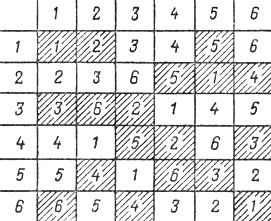
Рис. 30

Для того чтобы представить себе объем материала, среди которого проводится поиск требуемых латинских квадратов, сошлемся на Риордана [22]. Обозначим через l_n число латинских квадратов порядка n, элементы первой строки и первого столбца которых упорядочены в естественном порядке: 1, 2, ..., n. Тогда число L_n различных латинских квадратов порядка n составит

так как при произвольной перестановке строк (столбцов) латинский квадрат не утрачивает своих свойств.

При этом значения l_n для n≤7 таковы: