9. О спортивных классификациях

9.1. Принципы построения спортивных классификаций

Всякая спортивная классификация, основанная на упорядочении спортсменов по их силе (по результатам соревнований), связана с присвоением каждому из них определенной оценки, выражающейся в виде числа очков, набранных в турнирах, или в виде так называемого рейтинга - условного числового коэффициента.

В пределах отдельных соревнований этими оценками служат очки, набираемые участниками. Именно так обстоит дело в соревнованиях по спортивной и художественной гимнастике, фигурному катанию, в тяжелой атлетике и т. п.

Однако в спортивных играх, таких, например, как шахматы, теннис, бадминтон, целесообразно иметь не разовую, а интегральную оценку, в которой учитываются (в определенном смысле суммируются) результаты серии встреч с различными противниками в разных турнирах на протяжении определенного отрезка времени. Такие интегральные оценки используются в шахматных, теннисных и других классификациях. Рассмотрение действующих классификационных систем позволяет сделать некоторые заключения общего характера о принципах их построения.

Остановимся на системе классификации на основе рейтингов.

Оставим пока открытым вопрос о том, какие соображения учитываются при присвоении игрокам, входящим в классификацию исходного рейтинга (исходного места в классификации). Предположим, что вопрос этот тем или иным способом решен,

Рассмотрим встречу двух игроков. Обозначим оценки класса, т. е. рейтинги игроков U и V через r(U) и r(V) соответственно.

Введем в рассмотрение переменную величину t, характеризующую различие в классе игроков U и V. Величину t можно предположить зависящей, например, от отношения r(U)/r(V) рейтингов игроков U и Кили же от их разности r(U) - r(V).

В качестве исходного примем предположение, согласно которому отношение m/n среднего числа m побед игрока U к среднему числу n его пораженки в сериях из N встреч с игроком V находится в экспоненциальной зависимости от разности рейтингов игреков U и V.

Естественность такого предположения подтверждается статистическими данными о результатах шахматных турниров, теннисных и других игровых спортивных соревнований, а также, что не менее убедительно, нашими последующими результатами.

Итак, мы принимаем, что

где основание a экспоненты a^t - некоторое число, большее единицы, a t = r(U) - r(V), В этих обозначениях вероятность Р (победа U) победы игрока U в рассматриваемой встрече игроков U и V равна отношению среднего числа выигрываемых U встреч к общему числу встреч с игроком V, т. е.

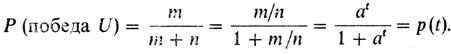
Ясно, что величина Р (победа U) является функцией t. Так как переменная t равна разности r(U) - r(V) рейтингов соперников, то непосредственно видно, что при t = 0 (т. е. при равном классе игроков) вероятность P(0) = 1/2: обе противоборствующие стороны могут выиграть встречу с равной вероятностью.

При неограниченном увеличении t (т. е. при неограниченном возрастании рейтинга игрока U по сравнению с рейтингом игрока У) вероятность P(r) стремится к единице: игрок U почти наверняка выиграет у У Если же t становится отрицательным (r (U)<r(V)) и неограниченно убывает, то вероятность P(t) победы U над V неограниченно приближается к нулю.

Графики функций P (t) в зависимости от значения параметра a показаны на рис. 31. График функции 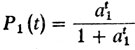расположен при a₁>a выше графика

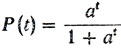
при t>0 и ниже его при t<0.

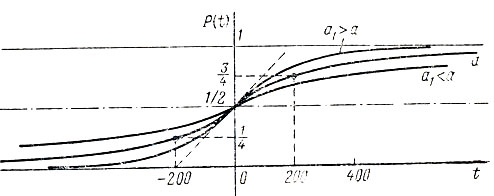
Рис. 31

Теперь вся проблема построения классификации сводится к выбору числового значения параметра a и масштаба для оценивания разности в классе (рейтингов) игроков.

С этой общей позиции можно объяснить идею построения уже ставшей классической (но пока не получившей в публикациях четкого обоснования) системы классификации шахматистов, предложенной американским профессором А. Эло и принятой Международной федерацией шахмат (ФИДЕ) в 1970 г.

Статистика шахматных турниров свидетельствует о том, что если один из соперников на один разряд (на одну ступень) в шахматной иерархии стоит выше другого, то первый выигрывает у второго, в среднем, 75 очков из 100 возможных, т. е. с вероятностью, равной 0,75.

При построении кривой p(t), т. е. при выборе значения параметра a, этот факт следует учесть следующим образом. Предположим, что различие между игроками, принадлежащими к двум соседним ступеням (разрядам) шахматной иерархии, составляет λ единиц рейтинга. Иными словами, при t = r(U) - r(V) = λ величина вероятности победы U над V равна P(λ) = 0,75. Это предположение приводит к соотношению для определения значения a:

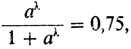
или a^λ = 3. Допустив, например, что λ = 200 из a²⁰⁰ = 3, найдем a = 1,0055.

Теперь можно подсчитать, что при разности рейтингов t = 5

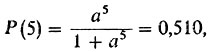
при t = 10 P(10) = 0,514; при t = 15 P(15) = 0,520; при t = 20 P(20) = 0,527 и т. д.

Подсчитав соответствующие вероятности P(t) для разностей рейтингов в пределах от t = 0 до t = 735 (и больше), придем к таблице A. Эло (табл. 10) (она приведена, например, в [24]).

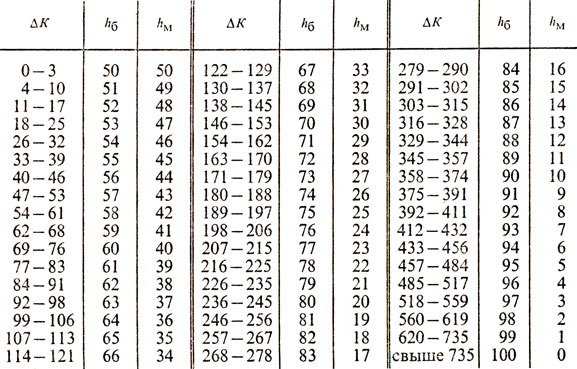
Таблица 10

Величина ΔK - разность между коэффициентами Эло игроков равна в наших обозначениях значению t. Величины h_δ и h_М из таблицы Эло (проценты, которые «полагается» набрать шахматисту с большим и, соответственно, с меньшим рейтингом) являются в действительности найденными выше вероятностями P(победа U) и P(победа V) = 1 - P (победа U),

Полученное совпадение говорит о том, что в качестве отправной разницы в рейтингах в системе Эло принято число 200.

Подчеркнем, однако, что можно предположить, вопреки Эло, что разница λ в рейтингах между представителями двух соседних ступеней шахматной иерархии должна составлять не 200, а, скажем, 250 (или даже 300) единиц рейтинга. Это привело бы к другому, меньшему значению параметра a = 1,0044, определяемому из уравнения a²⁵⁰ = 3, и, естественно,- к другой таблице, подобной, однако, таблице Эло.

Весьма возможно, что пересчет рейтингов игроков после завершения турнира с помощью новой таблицы окажется более удачным, чем по таблице Эло. Единственным обоснованием («оправданием»!) выбора значения λ = 200 может послужить изучение объемного статистического материала, накопленного в многолетних шахматных баталиях.

Так или иначе, имеется возможность построения целого семейства классификаций, подобных друг другу. Так, в частности, можно предполагать, что разница в рейтингах между представителями каждых двух соседних разрядов не должна быть постоянной, а меняться по мере продвижения вверх (от третьего разряда до гроссмейстера). Правда, это несколько усложнит процесс пересчета рейтингов и потому вряд ли окажется практически целесообразным.

Но вернемся к системе Эло. Она завершается правилом пересчета рейтинга шахматиста. Это правило формализуется в виде линейной зависимости

выражающей новый рейтинг (по завершении всего турнира) r_н через старый рейтинг r_ст (предшествующий турниру) и через разность между числом N очков, фактически набранных шахматистом, и числом очков N_ож, которое ему «полагается», в силу его квалификации, набрать в турнире.

Если фактически набранное число N очков совпадает с ожидаемым N_ож, то из (1) следует, что рейтинг шахматиста остается без изменения: r_н = r_cn.

При N>N_ож, т. е. при N - N_ож > 0, его рейтинг возрастет, при N <N_ож - станет меньше предматчевого.

В системе Эло в качестве коэффициента μ выбрано число 10. Поэтому при N - N_ож = 1 из формулы

следует, что рейтинг игрока возрастет на 10 единиц. Иными словами, одному очку, набранному сверх ожидаемых, соответствует 10 единиц рейтинга. Это обстоятельство является также своего рода «произволом». Можно положить, например, μ = 15 или μ = 20.

Реализация пересчета рейтинга требует знания величины N_ож. Числовое значение N_ож находится следующим способом (оно всегда округляется до полуочка и потому рейтинги всегда оказываются целыми числами).

Допустим, что шахматист A, имевший рейтинг r_ст (А) = 2280, встретился в турнире с игроками В, С, D, E, имевшими рейтинги соответственно равные: r_ст (B) = 2280, r_ст(C) = 2285, r_ст (D) = 2270, r_ст (C) = 2260. Тогда вероятность победы А над В составит 0,5 (отождествляется со средним числом выигранных очков), вероятность победы А над С равна 0,49 (так как r_ст(С) - r_ст(A) = 5), вероятность победы А над D равна 0,514 (так как r_ст(A) - r_ст(D) = 10), и, наконец, вероятность победы А над E равна 0,527 (так как r_ст(А) - r_ст(E) = 20). Следовательно, можно ожидать, что шахматист А во всех упомянутых встречах наберет

N_ож(A) = 0,500 + 0,490 + 0,514 + 0,527 = 2,031 очка.

Подсчет N_ож упрощается путем введения так называемого рейтинга r(m) турнира, равного среднеарифметическому рейтингов всех его участников.

Очевидно, что чем сильнее состав играющих, тем рейтинг турнира больше. Вообще, для рассмотрения (квалификации) турнира в системе Эло требуется, чтобы не менее двух третей его участников состояло в квалификационных списках (т. е. уже обладали присвоенными им рейтингами) до начала турнира и чтобы рейтинг турнира был не меньшим 2250.

Вступающему в турнир шахматисту, еще не обладающему рейтингом, присваивается начальный рейтинг r_нач = 2200.

Вслед за этим, вместо того чтобы находить значения параметра t для всех встреч A, B, C, D, E (как это сделано выше), его находят лишь единожды, как разность r_ст (А) - r (t) между рейтингами шахматиста А и турнира. Этим самым предполагают, что шахматист играет n - 1 партию (при n участниках) с некоторым фиктивным партнером, обладающим рейтингом r(т) турнира.

Так, например, допустив, что в турнире играют только шахматисты А, В, С, D, Е, найдем рейтинг турнира r(т) = ¹/₅ (2280 + 2280 + 2285 + 2270 + 2260) = 2275.

Шахматист А имеет рейтинг r_ст (A) = 2280. Разность t = 2280 - 2275 = 5. Раньше уже было подсчитано, что P(5) = 0,510. Так как А встречается с фиктивным партнером в четырех партиях, то для него ожидаемое число очков N_ож(A) = = 0,510×4 = 2,040 ≈ 2.

Допустим далее, что фактически А набрал в турнире N (А) = 3,5 очка. Тогда r_н(А) = 2280 + 10(3,5 - 2) = 2280 + 15 = 2295, и, следовательно, рейтинг А возрос на 15 единиц.

Классификационная система Эло основана, как можно заключить из предшествующего, на трех предположениях:

1. отношение среднего числа выигранных к общему числу сыгранных шахматистом со своим противником партий находится в экспоненциальной зависимости от разности рейтингов играющих сторон;
2. разница в рейтингах шахматистов двух соседних разрядов шахматной иерархии составляет 200 единиц рейтинга;
3. одному набранному (свыше ожидаемого числа) очку соответствует 10 единиц рейтинга.

Таким образом, система Эло имеет определенное Теоретико-статистическое обоснование. Ее правомерность подтверждена статистической достоверностью прогнозов.

Еще за семь лет до принятия ФИДЕ его системы (в 1963 г.) Эло подсчитал рейтинги выдающихся шахматистов со времен П. Морфи (рейтинг - 2690). При этом рейтинг r ≥ 2600 получили 28 шахматистов (Э. Ласкер, X. Капабланка, М. Ботвинник, М. Таль и др.).

Для того чтобы получить звание, например, международного мастера (гроссмейстера), правила ФИДЕ требуют повторного набора нормативного количества очков, зависящего от категории сложности турниров, в которых эти очки набираются.

В зависимости от рейтинга различают турниры шестнадцати категорий сложности.

Первая категория определяется рейтингом в диапазоне от 2251 до 2275. Шестнадцатая категория соответствует рейтингу в пределах 2626-2650.

Претендующий на звание международного мастера (гроссмейстера) должен набрать, например, в турнире десятой категории сложности (рейтинг 2476 - 2500) не менее 47 (соответственно 67) процентов максимально возможного числа очков.

Повторно нормативное количество очков претендующий может набрать в турнире иной категории сложности - в согласии с принятой ФИДЕ шкалой.

В принятой ныне в СССР классификации шахматистов, основанной на системе Эло, подсчет рейтингов (коэффициентов) отличается тем, что

1. ожидаемое количество очков N_ож округляется до 0,1 очка;
2. действует своя шкала сложности турниров и свои нормативы, достижение которых необходимо для получения спортивных званий;
3. для участника соревнований, обладающего исходным рейтингом r_ст = 2200, новый рейтинг r_н устанавливается по правилу
   r_н = 2100 + 200 ^N/_NM,
   где N_М - нормативное число очков мастера, а N - фактически набранное участником количество очков. Это правило позволяет удачно выступившему участнику значительно повысить свой рейтинг. Так, например, при выполнении им нормы мастера рейтинг его возрастет на 200 единиц.