
8.2. Круговая система

Эта система широко практикуется в футбольных, хоккейных, баскетбольных и теннисных соревнованиях. Если игры идут в два или в три круга, то результаты их можно считать весьма убедительными. Результаты завершенного турнира участников по круговой системе можно представить не только в виде сводной таблицы, но и в виде графа. Вершины графа (число их n) соответствуют участникам. Каждая пара вершин соединена ребром; всего ребер n(n - 1)/2. Такой граф называют полным. Если участник A
В теннисных встречах (как, впрочем, и в баскетболе, и в волейболе) ничьих не бывает. Круговой турнир в этих видах спорта оказывается «бескомпромиссным». Подобному турниру соответствует полный ориентированный граф. В качестве примера на рис. 27 представлены все возможные графы бескомпромиссных турниров с четырьмя участниками. Подобного рода (и аналогичные им) графы турниров специально изучаются математической дисциплиной (тесно связанной с комбинаторикой) - теорией графов (см., например, [21]).
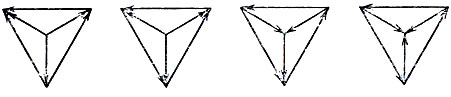
Рис. 27
При проведении шахматных турниров по круговой системе строго придерживаются расписания игр. Порядок встреч по турам и цвета фигур, которыми шахматисты играют в этом турнире, определяются номерами, полученными ими при жеребьевке. При этом для подсчетов используют специальные правила, предложенные немецким шахматистом Й. Бергером.
Поясним суть этих правил. Допустим, что число участников n четное. Рассмотрим какую-либо пару участников. Если номера s, t (по жеребьевке) каждого из них отличны от n, то номер тура, в котором они встречаются, равен Nst = s + t - 1 при s + t < n и равен Nst = s + t - n при s + t > n. Если сумма s + t - число нечетное, то белыми играет шахматист, имеющий меньший номер, а если сумма четная, то белыми играет его противник. Например, в турнире из восьми участников (n = 8) второй участник (s = 2) играет белыми с пятым (t = 5) в шестом туре (2 + 5 = 7 - нечетное число, меньшее восьми; 2 + 5 - 1 = 6). В то же время третий номер с седьмым играет черными во втором туре (3 + 7 - четное число, большее восьми; 3 + 7 - 8 = 2). Для участника с номером n расписание игр оказывается следующим. Номер тура, в котором он встречается с участником под номером l, равен 2l - 1 (при 2l<n) и 2l - n (при 2l > n). При этом с участниками под номерами от 1 до n/2 включительно он играет черными, а с остальными - белыми.
При нечетном и к числу участников присоединяют «фиктивного» игрока и сводят задачу составления расписания к четному случаю n + 1. Партии с фиктивным партнером не играются, а истинный участник в соответствующем туре свободен от игры.
Заметим, что при четном и участники с номерами от 1 до n/2 играют каждый на одну партию белыми больше (за счет встреч белыми с игроком под номером n), чем остальные. Поэтому при жеребьевке предпочтительными оказываются номера, не превосходящие n/2.
Такого же строгого порядка придерживаются теперь при организации теннисных соревнований по круговой системе.
Так, например, в классификационных соревнованиях по группам из шести участников игра белыми (в шахматах) ассоциируется с обеспечением встречи новыми мячами за счет соответствующего участника (в теннисе).
Изучение игр по круговой системе приводит ко многим интересным математическим задачам.
Вот простейшая из них. Известно, что в круговом турнире теннисистов двое имеют равное число побед. Можно ли всех участников упорядочить по силе игры? Оказывается, что нельзя, так как среди участников всегда найдутся трое A, B, C таких, что А выиграл у В, В выиграл у С, а С обыграл А (в соответствующем графе найдется так называемый ориентированный цикл). Действительно, в качестве А и В рассмотрим игроков с равным к числом побед, и пусть А обыграл В. Предположим, что В имеет победы над игроками C1, ..., Ck. Тогда ясно, что среди них имеется по крайней мере один, победивший А. Иначе у А было бы побед не меньше, чем k + 1. Этим все доказано. Любопытные ситуации, связанные с шахматными баталиями, описаны Е. Я. Гиком в [24].
Приведем две из них.
1. В турнире участвует n шахматистов. Какой максимальный разрыв в набранных очках может возникнуть между двумя участниками, занявшими соседние места?
Допустим, что максимальный разрыв в очках имеют участники, занявшие места s и s + 1. Шахматисты, занявшие первые s мест, сыграли между собой s(s - 1)/2 партий и набрали в общей сложности такое же количество очков. Кроме того, они сыграли s(n - s) партий с занявшими места с s + 1 по n и набрали при этом не более чем s(n - s) очков. Таким образом, сумма очков, набранная участниками, занявшими s первых мест, не превосходит s/(s-1)/2 + s(n-s) = (2n-s-1)s/2. Поскольку участник, занявший место s, среди первых s шахматистов занял последнее место, то он набрал не более 1/s(2n-s-1)s/2 = 2n-s-1/2 очков.
Участники, занявшие места с s + 1 по n, сыграли между собой (n-s)(n-s-1)/2 партий и в общей сложности набрали столько же очков. Поскольку участник, занявший место s + 1, занял среди них первое место, то он набрал не менее 1/n-s(n-s)(n-s-1)/2 = n-s-1/2 очков.
Следовательно, максимальный разрыв в очках между участниками, занявшими места s и s+1, не превосходит 2n-s-1/2 - n-s-1/2 = n/2, Такой разрыв достигается, например, при условии, что победитель обыграл всех противников и набрал n - 1 очко, а остальные участники все партии между собой закончили вничью и набрали по n/2 - 1 очков. При этом (n - 1) - (n/2 - 1) = n/2.
В крупных шахматных соревнованиях с сильным составом подобный разрыв маловероятен. Однако в анналах соревнований отмечен единственный случай, когда Алехин в 1931 г. на турнире в Бледе оторвался от своих ближайших соперников на 5,5 очков.
2. В ряде случаев после завершения турнира возникает необходимость перенумеровать всех участников в таком порядке, чтобы ни один из них не имел поражения от следующего за ним участника.
Убедимся в возможности такого упорядочения участников. Для этого воспользуемся методом математической индукции. Для двух участников упорядочение очевидно. Предположим, что оно имеет место для произвольного турнира с т участниками. Обратимся к результату турнира с m+1 участником. Выберем любые m участников и упорядочим их требуемым способом (это возможно по индуктивному предположению). Затем выясним, как (m + 1)-й участник сыграл с первым. Если он выиграл или сыграл вничью, то поставим его на первое место. Если же проиграл, то выясним, каков его результат в игре со вторым и т. д. Если в ходе, подобного перебора придем к участнику, у которого (m + 1)-й выиграл или сыграл вничью, то поставим (m + 1)-го перед ним. В противном случае (т. е. когда (m + 1)-й участник всем проиграл) ставим (m + 1)-го на последнее место.
В соревнованиях шахматистов с большим числом участников используется швейцарская система. Вначале проводится жеребьевка. В первом туре играют шахматисты с номерами m и m + 1 (m = 1, 2, ...), причем участники с нечетными номерами играют белыми. В последующих турах играют между собой участники, набравшие равное количество очков. Если в одной из таких групп оказывается нечетное число участников, то смешивают соседние группы. Жеребьевку проводят с таким расчетом, чтобы каждый участник (в лучшем случае) от тура к туру менял цвет своих фигур или же, по крайней мере, равное число партий играл фигурами разных цветов.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'