7.8. «Полосатые ребята» - «Липовый лист» (на хоккейную тему)

Приводим репортаж из газеты «Ыхо» от 31 апреля 198.. года.

«Как обычно, в конце сезона состоялся хоккейный матч сборных двух стран за переходящий серебряный кубок континента. Встреча протекала в упорной борьбе: первый период выиграли «Полосатые ребята» со счетом 3:1, а после второго счет стал 4:3 в их же пользу. Третий период начался со штурма ворот «Полосатых» и в середине периода «Липовый лист» сравнял счет. Игровое преимущество целиком перешло в руки «Липовых», однако они никак не могли забить решающий гол.

За пять минут до конца игры зрители начали недоумевать по поводу необычной чехарды пятерок команды «Липовый лист», которую организовали тренеры. Они перестали выпускать на лед четвертую пятерку, реже стала появляться и первая пятерка, зато вторая и третья не успевали менять друг друга. Недоумение, начавшиеся было крики типа «Сапожники!», «Тренеров в салат!» сменились ревом восторга: за полторы минуты до конца встречи был забит решающий гол! Со счетом 5:4 победила команда «Липовый лист» и в четвертый раз подряд завоевала переходящий приз.

На состоявшейся после матча пресс-конференции тренер команды «Липовый лист» сказал, что победой они целиком и полностью обязаны молодому математику, начавшему работать в команде в конце сезона. Заявление тренера вызвало сенсацию. Защелкали затворы фотокамер, засверкали блики вспышек, несколько журналистов протянули свои микрофоны автору сенсации, прося объяснить, каким образом математика может помочь выиграть столь ответственный хоккейный поединок.

Вот что рассказал математик-консультант (приводим несколько упрощенное изложение рассказа о том, что же происходило на скамейке запасных в последнюю десятиминутку встречи):

«Наше преимущество было очевидным, но мы никак не могли реализовать его. Вроде бы все наши пятерки, а их было, как и обычно, четыре, вчистую переигрывали соперников, но шайба в ворота не шла. Тогда я решил, что надо попробовать перетасовывать пятерки так, чтобы выпускать их на лед случайным образом, не ожидая действия противника. Дело в том, что соперники устали значительно сильнее наших игроков, и медленные замены, когда каждый тренер выпускает то одну пятерку, то другую, играли на руку «Полосатым ребятам» и позволяли им сбивать темп наших атак. Я решил составить прямоугольную таблицу, строки которой предназначил нашим пятеркам, а столбцы - пятеркам «Полосатых». У нас четыре игровые пятерки, у противников осталось три (так как двое игроков из четвертой пятерки получили травмы). На пересечении строки, отвечающей нашей пятерке α_i и столбца пятерки β_j противника, проставил оценку a_ij (по десятибалльной шкале) игрового преимущества α_i перед β_j.

Оценку α_ij я получил в результате усреднения соответствующих индивидуальных оценок, бегло высказанных мне тренерами команды и примерно известных им по опыту предыдущих встреч.

Так как в последнее время при мне постоянно мини-ЭВМ, то я моментально составил следующую игровую таблицу (сразу же хочу подчеркнуть, что мог бы составить аналогичную таблицу, в которую в качестве a_ij заносил бы вероятность p_ij выигрыша пятерки α_i при встрече с пятеркой β_j):

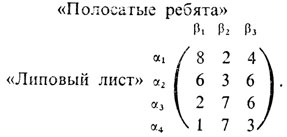
После этого я составил эквивалентную задачу линейного программирования с ограничениями (см. 7.7)

и линейной функцией

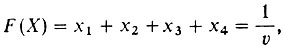
которую надо минимизировать. Напомню, что здесь v - цена (пока неизвестная) построенной мною матричной игры.

Не стану затруднять вас подробным решением полученной задачи линейного программирования, можете сами решить ее симплекс-методом, а сразу же сообщу ответ: оптимальное решение таково:

Таким образом, цена игры оказалась равной ³²/₇, а оптимальные вероятности использования чистых стратегий в смешанной стратегии тренеров моей команды (т. е. оптимальная стратегия «первого игрока» моей команды) определились следующим образом:

Именно поэтому мы стали реже выпускать первую пятерку, а четвертую и вовсе перестали включать в игру. Принимая во внимание то, что противная сторона не использовала свою оптимальную стратегию, при которой конец: матча ей лучше было бы проводить в две пятерки, посадив третью на скамейку запасных, мы вполне естественно превратили свое преимущество в решающий гол!»

После такой беседы тренерам следует задуматься над проблемами, возникающими в хоккейных встречах.