
7.9 Формирование команды пловцов

Одно из первых предложений по использованию алгоритма решения задачи о назначениях (см. п. 6.1) для формирования команды изложено в 1970 г. в работе Maxhol R. Е. An Application of the Assignment Problem.- Oper. Res., 1970, v. 18, № 4, p. 569-760. В ней шла речь о формировании команды для смешанной эстафеты по плаванию из группы спортсменов, среди которых имеется несколько спортсменов, хорошо владеющих более чем одним стилем плавания.
В смешанной эстафете участвуют четверо спортсменов, из которых каждый проплывает дистанцию только одним, определенным заранее, стилем (брасс, баттерфляй, на спине, кроль) и в определенной последовательности.
Усложненная задача формирования основного состава из 38 кандидатов рассматривалась в 1972 г. В упомянутой работе изложена хорошо продуманная, но довольно сложная методика определения коэффициентов целевой функции (в наших обозначениях - элементов матрицы баллов Г). Сначала тренер составляет реестр показателей (физиологических, интеллектуальных, психологических и др.), которыми должен обладать претендент, с тем, чтобы во время тренировок занять в эстафете определенное порядковое место. Из этого реестра производится выборка и показателей, исключающих (по возможности) друг друга, но вместе с тем достаточно характеризующих спортсмена. Тем самым определяются «независимые» показатели качества спортсмена. Затем каждый тренер оценивает значимость каждого показателя, придавая ему определенный «вес» (числовой множитель) с учетом места, занимаемого игроком в процессе тренировок. Далее, тем или иным способом, принятым в экспертных оценках (см. п. 4.1), вычисляется коллективный весовой множитель. В итоге возникает «весовая» матрица Λ = (λij) размерности n×m. Ее элемент λij - это вес, приписываемый тренерами i-му показателю i = 1, ..., n) при условии, что спортсмен занял j-е место в команде (j = 1, ..., m).
На следующем этапе лицо, принимающее решение (например старший тренер), определяет значимость каждого из m мест в составе команды, вновь используя методику весовых множителей, j-му месту приписывает вес μj (j = 1, ..., m). Вслед за этим тренерский состав оценивает каждого из k пловцов. С этой целью строят весовую матрицу A = (aij) размерности k×n, в которой aij - вес i-го пловца по i-му показателю. В результате умножения матрицы Ak×n на матрицу Λn×m возникает матрица Г (γij)k×m = Ak×nΛn×m. Ее элемент γij = ai1λ1j + ai2λ2j + ... + ainλnj Дает оценку значимости для команды того факта, что i-й пловец займет j-е место (i = 1, ..., k; j = 1, ..., m).
Оценка вклада в общее выступление команды i-м пловцом на j-м месте дается показателем δij = γijμj. Приходим к матрице Δk×m = (δij). Все завершается решением уже известной нам задачи о назначениях методом линейного программирования. Вводят переменные xij = 0 или 1 (в зависимости от того, поставлен ли i-й пловец на j-е место или нет); записывают известную систему ограничений:
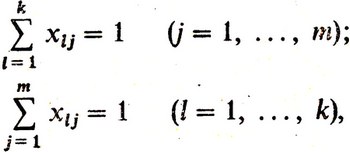
и, при условии их выполнения, максимизируют целевую функцию - эффективность выступления всей команды
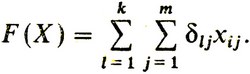
Практическое решение этой задачи в конкретных случаях может быть достигнуто, например, симплекс-методом (см. п, 6.8) с помощью ЭВМ.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'