7.7. Матричные игры и линейное программирование

Рассмотрим антагонистическую игру с матрицей выигрыша A = (a_ij) размерности m×n:

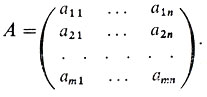
Пусть вектор вероятностей x = (x₁, x₂, ..., x_m) (где x_i ≥ 0 при всех i = 1, ..., m, и 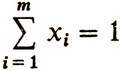) есть некоторая оптимальная стратегия первого игрока. Тогда, применяя против нее любую свою стратегию, второй игрок не сможет помешать первому выиграть v или даже больше, чем v, где v - цена игры (вспомним теорему о минимаксе!), пока нам неизвестная. Таким- образом, можно записать неравенства

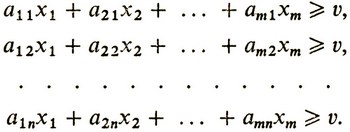
Кроме того, можно учесть условие нормировки вектора х:

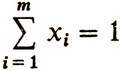
Предположим, что цена игры v отлична от нуля (больше нуля). В противном случае прибавим ко всем элементам матрицы А одно и то же достаточно большое число и тем самым увеличим цену игры на это же число. Оптимальные стратегии при этом не изменятся. Затем, разделив неравенства и условие нормировки на величину v, получим

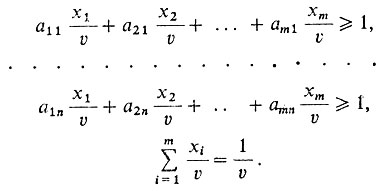
Теперь введем новые переменные

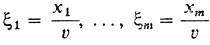
и заметим, что цель первого игрока увеличить величину v и соответственно уменьшить величину 1/v. Таким образом, мы пришли к следующей задаче линейного программирования с ограничениями в виде неравенств: минимизировать сумму

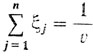
при ограничениях

Читатель уже успел познакомиться с методом решения подобных задач (задач линейного программирования) и сумеет найти значения ξ_j (следовательно, и x_j) составляющие оптимальную стратегию первого игрока.

Отметим, что при решении конечных игр с большим числом стратегий часто используют приближенные (итеративные) методы. К настоящему времени разработано достаточно много несложных итеративных процедур, которые легко укладываются в программу для ЭВМ и приводят к оптимальным стратегиям.

Теперь - хоккей!