7.6. Железная игра

Сказания многих народов повествуют о героях, обладающих необычной силой, способных справляться с подъемом и переносом предметов огромного веса. К далеким временам восходят всевозможные силовые упражнения, различного рода народные состязания по подъему тяжестей, метанию тяжелых предметов и подобные им. На этой базе возник вид спорта, называемый ныне тяжелой атлетикой.

Чемпионаты Европы по тяжелой атлетике проводятся ежегодно с 1896 г., чемпионаты мира - с 1898 г. В 1920 г. создана Международная федерация тяжелой атлетики (ИВФ). Одновременно с созданием федерации тяжелая атлетика стала олимпийским видом спорта.

Снарядом, используемым в соревнованиях, служит штанга: гриф с насаживаемыми на него различного веса дисками.

Соревнования по современной тяжелой атлетике проводятся по системе олимпийского двоеборья. Олимпийское двоеборье состоит из последовательного выполнения двух упражнений: сначала рывка, а затем толчка штанги обеими руками.

При рывке штанга в быстром темпе поднимается и удерживается выпрямившимся спортсменом на вытянутых руках над головой.

Выполнение толчка состоит из двух этапов: сначала штанга поднимается на грудь, а затем толчковым движением поднимается от груди и удерживается на вытянутых руках над головой.

Возможности штангиста существенно зависят от его собственного веса, поэтому соревнования проводятся отдельно по каждой из десяти весовых категорий (вне зависимости от возраста спортсмена).

Каждый участник соревнований имеет право на три попытки для выполнения рывка и на три - для выполнения толчка. Атлет объявляет судьям вес, с которого он начинает соревнования.

Однако первую попытку атлет может выполнять со штангой как большего, так и меньшего веса по сравнению с объявленным. После успешной первой попытки вес штанги увеличивается не менее, чем на 5 кг. При переходе от успешной второй попытки к третьей вес штанги повышается не менее, чем на 2,5 кг. Если все три попытки оказались успешными, штангисту предоставляется возможность в четвертой попытке установить рекорд. При этом вес штанги должен быть по крайней мере на 0,5 кг выше рекордного. Результат четвертой попытки не идет в зачет соревнований.

В личных соревнованиях победитель определяется по сумме результатов, показанных в двоеборье. Если одинаковый вес подняли несколько штангистов, то победителем считается тот, чей собственный вес до соревнований был меньшим. Если и эти веса одинаковы, то проводится повторное взвешивание после соревнований. В случае повторного совпадения результатов взвешивания спортсмены делят одно и то же призовое место.

На международных и национальных соревнованиях судейская коллегия формируется из главного судьи, двух боковых судей, секретаря и судьи-информатора, ведущего одновременно учет времени (с момента вызова спортсмена на помост до подъема им штанги должно пройти не более трех минут). Все спорные вопросы решает жюри из трех или пяти членов.

Рассмотрим теперь соревнования штангистов с позиции математической теории игр.

Предположим, что в соревновании участвуют два основных соперника: I и II. При этом по жребию штангисту I приходится выходить для поднятия каждого веса раньше, чем его основному сопернику - штангисту II. Согласно правилам соревнований каждый атлет может либо попытаться поднять штангу заданного веса, либо пропустить свой подход и ждать увеличения веса штанги, после чего он опять-таки может либо пропустить свой выход к этому весу, сохранив его для еще большего, либо попытаться поднять штангу. Простоты ради положим, что каждый штангист имеет право только на одну попытку и на один пропуск на любом весе. Наличие трех попыток не влияет принципиально на построенную ниже модель, а только увеличивает число описываемых ситуаций. Отметим, что и этот случай не очень сложно проанализировать с помощью ЭВМ.

Допустим, что начальный вес 200 кг, вероятность того, кто его поднимет первый штангист, равна p₁, а что поднимет второй - q₁, соответствующие вероятности для веса 202,5 кг составят p₂ и q₂ и т. д. В этом случае игру можно описать в виде графа-дерева, представленного на рис. 25.

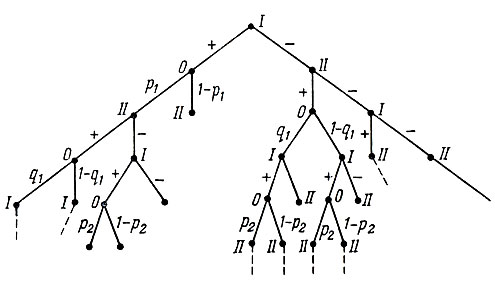
Рис. 25

Если у вершины нанесена цифра I, то это означает, что в этой ситуации ходит (т. е. делает попытку, или пропускает вес) первый игрок, если проставлена цифра II - то ходит второй, а если нанесен 0, то работает "случайный механизм", а именно: с вероятностью p_k или q_k k-й вес (200 кг + k*2,5 кг) взят, и с вероятностью 1 - p_k (или 1 - q_k) он не поднят. Знак " + " у дуги соответствует тому, что соответствующий штангист (эта дуга выходит из вершины, помеченной соответствующим номером) решил провести попытку, а знак "-" тому, что он ее переносит на более тяжелый вес. Ясно, что построение графа можно продолжить. При этом, естественно, надо помнить, что вероятности p_k и q_k резко убывают с ростом веса штанги.

Игры, заданные в виде такого графа-дерева, называются играми в развернутой форме, или, чаще, позиционными играми. Такое название обусловлено тем, что в любой момент игры каждый из соперников знает ходы свои и чужие и знает, в какой вершине графа находится.

Чистой стратегией в такой игре называют такой набор действий, при котором каждой вершине графа соответствует одно определенное действие того из игроков, чей черед ходить. Известным математиком Цермело доказано, что в любой позиционной игре (в том числе и в позиционной игре со случайными ходами, как и в нашем примере) существует оптимальная чистая стратегия, т. е. такая наилучшая стратегия, которая указывает, что надо делать каждому игроку в зависимости от сложившейся в игре позиции (ситуации).

Мы не будем останавливаться на том, какова оптимальная стратегия в приведенном примере: ее нахождение связано с большим перебором различных вариантов, и без помощи компьютера практически это неосуществимо.

Отметим только, что для рассматриваемого случая при известных вероятностях p_k, q_k (k = 1, 2, ...) найти оптимальную стратегию можно. Нам кажется, что знание оптимального стратегического поведения штангиста и его тренера имеет колоссальное психологическое значение, так как дает уверенность в том, что уж по крайней мере тактического проигрыша не будет, хотя, конечно же, проигрыш соревнования в общем возможен.

В заключение этого небольшого раздела хотелось бы сказать, что для любой позиционной игры двух лиц существует эквивалентная ей матричная игра. Поэтому очень часто нахождение оптимального поведения в игре, заданной в развернутой форме, сводится к нахождению оптимальных стратегий в эквивалентных матричных играх.

Поясним нашу мысль и рассмотрим в качестве примера пусть несколько упрощенную, но любопытную ситуацию. Допустим, как прежде, что каждый из двух соревнующихся спортсменов имеет право одной попытки подъема штанги и пропуска лишь одного веса в поднятии штанги. Предположим также, что состязания начинает первый штангист (I), что он легче второго (II) и что оба уже взяли равный вес. В этом случае граф-дерево имеет вид, показанный на рис. 26. Заметим, что +1 означает выигрыш первого, а -1 означает выигрыш второго из штангистов. Напомним вновь, что естественно предположить: p₂<p₁ и q₂<q₁.

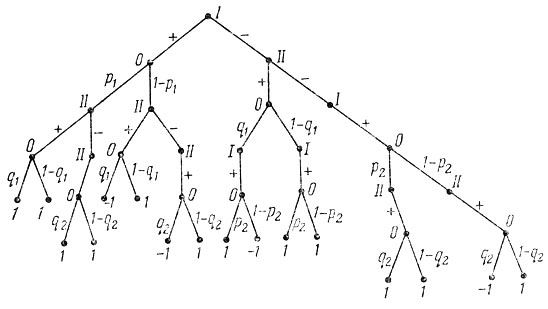
Рис. 26

Рассмотрим ситуацию с точки зрения первого штангиста. Если штангист I решит брать первый вес и возьмет его, то штангисту II для победы необходимо попытаться поднять следующий вес, так как штангист II тяжелее. Если же штангист I не поднимет первый установленный вес, то штангисту II, очевидно, надо заказывать тот же вес, так как для него вероятность q₁ поднять этот вес больше вероятности q₂ поднять следующий.

Оценим выигрыш штангиста I в случае, если он решает поднять начальный вес. Этот вес он поднимет с вероятностью p₁; в таком случае штангист II, зная этот результат, решит поднимать следующий - больший вес, вероятность поднять который q₂. Значит, в этом случае ожидаемый выигрыш штангиста I составит

С вероятностью 1 - p₁ штангист I не поднимет начальный вес, а штангист II его поднимет с вероятностью q₁, или не осилит с вероятностью 1 - q₁. В этом случае выигрыш первого будет равен

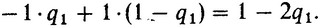
Таким образом, если штангист I собирается использовать попытку на начальном весе, его ожидаемый выигрыш v₁( + ) (математическое ожидание выигрыша) вычисляется по следующей формуле:

Ясно, что выигрыш v₂ штангиста II в этом случае равен - v₁(+). Теперь допустим, что штангист I решает пропустить первый подход. В этом случае он как бы меняется ролями со штангистом II и ждет, что тот будет делать. Если штангист II решит поднимать начальный вес, то он его осилит с вероятностью q₁, или не осилит с вероятностью 1 - q₁. В первом из этих двух случаев вероятность победы штангиста I равна p₂, а во втором - единице (штангист I легче). Таким образом, если штангист II попытается использовать первый подход, то средний выигрыш штангиста I в этом случае составит

Если же штангист II будет пытаться использовать второй подход (т. е. пропустит первый), то он с вероятностью q₂(1 - p₂) выигрывает, а с вероятностью (1 - q₂) проигрывает штангисту I. Значит, в этой ситуации

Естественно предположить, что штангист II изберет такое поведение, при котором его выигрыш минимизируется. Иными словами, сначала он найдет минимум из двух величин v₂(+) и v₂(-), а затем поступит так: он использует первую попытку, если v₂(+)<v₂(-), или же использует подход на большем весе, если v₂(+)>v₂(-). Сравним эти две величины:

Найдем их разность

Так как q₁>q₂, а p₂<1, то отсюда заключаем, что - v₂(+)<-v₂(-) или, окончательно, v₂(-)>v₂(+). Таким образом, штангисту II также выгодно пропустить первый вес, коль скоро его пропускает штангист I.

В этой задаче оптимальная стратегия штангиста I состоит в выходе к первому весу, если v₁(+)>v₂(-), и в необходимости пытаться поднять более тяжелый вес, если v₁(+)><v₂(-).

Оптимальное поведение штангиста II состоит в следующем. Если первый пропускает вес, то и второму необходимо также пропускать этот вес, что в рассматриваемой ситуации объясняется тем, что сам он тяжелее соперника. Если же первый штангист пытается поднять более легкий вес, то второй должен поднимать тот же вес, если попытка первого участника не удалась, и идти на больший вес, если выход первого штангиста был удачен.

Анализ решения приведенного примера не внес ничего нового в тактику выступления того из спортсменов, который "ходит" вторым. Однако, как нам кажется, этот анализ позволяет выработать тактику поведения штангиста в ответственных соревнованиях в тех случаях, когда он должен "ходить" первым или (при нескольких участниках) начинать выступление раньше своего основного соперника. Нетрудно увидеть, что в любой ситуации тому штангисту, чей выход предусмотрен раньше, следует правильно оценить свое решение: "ходить" или "пропускать"; в то же время решение второго штангиста более очевидно. Именно это обстоятельство побудило нас рассмотреть сравнительно несложную тактическую задачу с позиции участника, которому приходится подходить к весу ("ходить") первым.