
7.5. Как смазать лыжи

Рассмотрим следующую задачу. Тренерский коллектив лыжной команды обсуждает, как всегда, вариант мази для лыж. Тренеры знают, что во время лыжной гонки погода (природа) может находиться в трех состояниях (β1, β2 и β3, а в их распоряжении имеется четыре типа лыжной мази α1, α2, α3 и α4. Матрица А вероятностей удачного прохождения трассы гонки спортсменами известна :

Другими словами, известно, что если будет использована мазь α3 и природа будет находиться в состоянии β2, то с вероятностью 0,8 эта мазь позволит пройти спортсмену дистанцию в полную силу. Аналогичный смысл имеют остальные элементы матрицы А. Какую же мазь следует выбрать?
Проще всего поставленная задача была бы решена тренерским коллективом, если бы были известны вероятности p1, p2, p3, с которыми погода "может находиться в каждом из трех возможных состояний. В самом деле, для этого достаточно найти математическое ожидание выигрыша для каждой мази и выбрать тот вариант, при котором средний ожидаемый выигрыш наибольший. Если бы в данном примере вероятность первого состояния природы p1 была равна 0,3, второго состояния - p2 = 0,5, а третьего - p3 = 0,2, то ожидаемые средние выигрыши были бы равны соответственно:
mα1 = 0,3*0,2 + 0,5*0,3 + 0,2*0,15 = 0,24,
mα2 = 0,3*0,75 + 0,5*0,2 + 0,2*0,35 = 0,395,
mα3 = 0,3*0,22 + 0,5*0,8 + 0,2*0,25 = 0,525,
mα4 = 0,3*0,85 + 0,5*0,05 + 0,2*0,25 = 0,33.
Таким образом, при таких вероятностях следовало бы использовать третий вариант смазки, а ожидаемый в этом случае выигрыш был бы наибольшим из всех четырех вариантов и равен 0,525.
К сожалению, вероятности состояний погоды тренерам были не известны (они не доверяли прогнозам бюро погоды), поэтому им пришлось на тренерском совете решать иначе опрос о том, какой мазью следует смазать лыжи. Заметим, то старший тренер был "рационалистом", один из его помощников - "пессимистом", а другой - "оптимистом". "Пессимист" считал, что из всех вариантов надо выбрать такой, при котором минимальный выигрыш будет максимальным, т. е. он предложил выписать все минимальные элементы строк: 0,15; 0,20; 0,25; 0,05. И из них выбрать максимальный элемент. В данном случае это 0,25, и соответствующая стратегия, предложенная "пессимистом", была α3.
Такой выбор предписан так называемым "максиминным" критерием Вальда.
В согласии с этим критерием оптимальной считается та стратегия α, для которой минимальный выигрыш максимален: maximminjaij. Таким образом, этот критерий ориентирован на худшие погодные условия и носит явно пессимистический характер.
После этого старший тренер команды предложил высказаться "оптимисту". Естественно, что "оптимист", рассчитывая, как всегда, на лучшее, предложил четвертый вариант смазки, так как соответствующий выигрыш при благоприятных условиях наибольший.
Старший тренер (он был человеком сведущим!), выслушав своих помощников, предложил использовать так называемый критерий пессимизма-оптимизма Гурвица. А именно, сначала выбрать величину 0≤λ≤1, а затем найти строку, для которой достигается
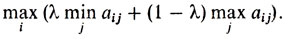
Легко видеть, что при λ = 1 - это критерий пессимизма Вальда, а при λ = 0 он превращается в критерий "крайнего оптимизма".
При промежуточном значении λ возникает "промежуточный" критерий: оптимистичней крайнего пессимизма и пессимистичней крайнего оптимизма. Числовое значение λ старший тренер предложил взять равным 0,6, делая скидку на возможное ухудшение погоды. После чего были найдены значения hi (i = 1, ..., 4) для каждой строки
h1 = 0,6*0,15 + 0,4*0,3 = 0,21,
h2 = 0,6*0,2 + 0,4*0,75 = 0,42,
h3 = 0,6*0,25 + 0,4*0,8 = 0,47,
h4 = 0,6*0,05 + 0,4*0,85 = 0,37.
Наибольшим является h3 = 0,47, и поэтому все склонялись к решению смазывать лыжи третьим вариантом смазки (стратегия α3). С точки зрения здравого смысла такое решение также достаточно оправдано, так как нельзя впадать при принятии стратегических решений ни в крайний оптимизм, ни в крайний пессимизм.
Казалось бы, вопрос уже решен. Однако в последний момент слово взял член тренерского совета, зарекомендовавший себя как "возмутитель спокойствия". По всякому вопросу он имел свое собственное мнение и зачастую высказывал неожиданные соображения. Вот и на этот раз он заявил, что для принятия решения не следует изучать элементы матрицы успехов. И вот почему. Во-первых, стратегию ах следует сразу же исключить из рассмотрения, так как она заведомо хуже стратегии α3. Действительно, каким бы ни оказалось состояние βj природы, вероятности успеха a11 = 0,20, a12 = 0,30, a13 = 0,15 меньше соответствующих вероятностей a31 = 0,25; a32 = 0,80; a33 = 0,25. Иными словами, первую строку матрицы А следует отбросить и работать с матрицей успехов меньшей размерности:

Во-вторых, и это особенно важно, вообще нет убедительных оснований для использования матрицы успехов в решении рассматриваемого вопроса. Так, например, успех a41 = 0,85 при стратегии α4 и состоянии природы β1 больше чем при стратегии α3 и состоянии β2. Однако выбор α4 может оказаться более удачным чем выбор α3 лишь потому, что состояние β1 благоприятнее, нежели состояние β2. Тем самым сравниваются наши решения в различных ситуациях βj. На самом же деле надлежит рассуждать так, чтобы суметь учесть, насколько благоприятствует нам каждое из состояний погоды при различных выборах αi. А именно: если бы мы заранее знали истинное состояние погоды βj, то выбор αi был бы предопределен. Просто в столбце для βj мы выбрали бы наибольший элемент, т. е. maxiaij. Обозначим его через cj = maxi aij. Составим теперь разность cj - aij = rij. Эта разность дает отклонение выигрыша aij, который мы получили бы при выборе стратегии αi (не зная заранее о состоянии природы βj) от максимально возможного выигрыша cj, получаемого нами при условии заблаговременной информации о том, что природа находится в состоянии βj. Поэтому разность rij естественно считать нашим "риском" при использовании стратегии αi при состоянии βj природы. И вместо матрицы A успехов значительно разумнее ориентироваться на матрицу R = (rij) рисков. С этой целью найдем
c1 = maxi ai1 = 0,85, c2 = maxi ai2 = 0,80, c3 = maxi ai3 = 0,45
и вычислим разности rij. Получим матрицу рисков

Сравним ее с матрицей А. В этой последней выигрыши a31 и a33 одинаковы и равны 0,25. Однако они далеко не равноценны, ибо при выборе стратегии α3 при состоянии природы β1 риск r31 = 0,60 окажется втрое больше риска r33 = 0,20 при той же стратегии α3, но в состоянии β3. В силу всех изложенных соображений "возмутитель спокойствия" настаивал на том, чтобы в тех условиях, когда состояние природы заранее не определено, стремиться лишь к одному - к уменьшению риска. Иными словами, следует выбирать такую стратегию, при которой величина риска окажется наименьшей в самой неблагоприятной ситуации. А для этого необходимо подсчитать 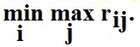
В наших условиях 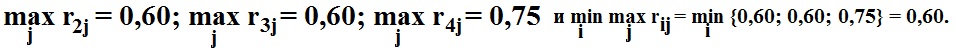 Следовательно, выбрать нужно стратегию α2 или α3, гарантирующие наименьший риск при любом состоянии природы (в наиболее неблагоприятной ситуации).
Следовательно, выбрать нужно стратегию α2 или α3, гарантирующие наименьший риск при любом состоянии природы (в наиболее неблагоприятной ситуации).
"Позвольте,- перебил выступающего старший тренер,- ведь ваше предложение в идейном плане немногим лучше предложения "пессимиста". Различие лишь в том, что согласно вашему критерию наихудшим следует считать не минимальный выигрыш, а максимальный риск. Но это хорошо известный в теории принятия решений так называемый "минимаксный" критерий Севиджа. Критерий этот столь же пессимистичен, как и "максиминный" критерий Вальда. Будем же придерживаться золотой середины и остановимся на стратегии α3. Что же касается возможных упрощений в матрице A путем отбрасывания стратегий, заведомо худших других, то с этим следует полностью согласиться". На этом обсуждение вопроса о смазке лыж завершилось.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'